题目内容
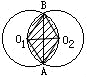
 如图,两个半径相等的圆相交,两圆的圆心相距正好等于半径,AB弦约等于17厘米,半径为10厘米,求阴影部分的面积.
如图,两个半径相等的圆相交,两圆的圆心相距正好等于半径,AB弦约等于17厘米,半径为10厘米,求阴影部分的面积.分析:(1)阴影部分由两个相等的弓形组成,我们只需要求出一个弓形面积,然后二倍就是要求的阴影面积了.由已知若分别连接AO1,AO2,BO1,BO2,O1O2,如图所示,就可以得到两个等边三角形(各边长等于半径),则∠AO2O1=∠BO2O1=60°,即∠AO2B=120°.这样就可以求出以O2为圆心的扇形AO1BO2的面积,
(2)然后再减去三角形AO2B的面积,就得到弓形面积,三角形AO2B的面积就是二分之一底乘高,底是弦AB,高是O1O2的一半.
(2)然后再减去三角形AO2B的面积,就得到弓形面积,三角形AO2B的面积就是二分之一底乘高,底是弦AB,高是O1O2的一半.

解答:解:分别连接AO1,AO2,BO1,BO2,O1O2,如图所示,就可以得到两个等边三角形(各边长等于半径),则∠AO2O1=∠BO2O1=60°,即∠AO2B=120°.
120°÷360°=
,
×3.14×102-17×(10÷2)÷2,
=
×3.14×100-17×5÷2,
≈104.67-42.5,
=62.17(平方厘米);
62.17×2=124.34(平方厘米);
答:阴影部分的面积是124.34平方厘米.

120°÷360°=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
≈104.67-42.5,
=62.17(平方厘米);
62.17×2=124.34(平方厘米);
答:阴影部分的面积是124.34平方厘米.
点评:连接圆心线,与图中的半径组成了两个等边三角形,从而得出弓形所对的圆心角的度数是解决此类问题的关键.

练习册系列答案
相关题目
 如图所示,在直角三角形ABC中,AB=6厘米,BC=15厘米,从中剪掉两个半径相等的扇形,求剩余部分的面积.
如图所示,在直角三角形ABC中,AB=6厘米,BC=15厘米,从中剪掉两个半径相等的扇形,求剩余部分的面积. (2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)
(2012?武汉模拟)如图,两个半径相等的圆A和圆B相交,三角形BCD是等腰直角三角形,其面积为60cm2,四边形ABCD是平行四边形,求图中阴影部分的面积.(π取3.14)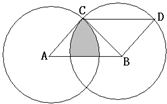 (2013?青羊区模拟)如图:两个半径相等的圆A和圆B相交,三角形DBC是等腰直角三角形,面积是24平方厘米,ABDC是平行四边形.图中阴影部分的面积是
(2013?青羊区模拟)如图:两个半径相等的圆A和圆B相交,三角形DBC是等腰直角三角形,面积是24平方厘米,ABDC是平行四边形.图中阴影部分的面积是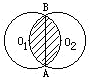 如图,两个半径相等的圆相交,两圆的圆心相距正好等于半径,AB弦约等于17厘米,半径为10厘米,求阴影部分的面积.
如图,两个半径相等的圆相交,两圆的圆心相距正好等于半径,AB弦约等于17厘米,半径为10厘米,求阴影部分的面积.