题目内容
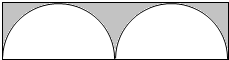
14. 如图,在圆周上有一些点,顺次用线段连接每隔开一个点的所有两点,结果通过圆周上所有的点,并且最后回到了原来的出发点.这样得到的图形的各个尖出的角(图中
如图,在圆周上有一些点,顺次用线段连接每隔开一个点的所有两点,结果通过圆周上所有的点,并且最后回到了原来的出发点.这样得到的图形的各个尖出的角(图中 的部分)的和是2700°.请问:圆周上有多少个点?
的部分)的和是2700°.请问:圆周上有多少个点?
分析 如图,假设有n个顶点,这n个顶点都是均匀分布,在内部就构成一个正n边形,由n内个角,∠1就是其中1个,根据正n边形每个角的度数是$\frac{(n-2)×180°}{n}$,所以∠1=180°-$\frac{360°}{n}$,每个小三角形都是等腰三角形,根据∠1与∠2、∠3的关系,求出用含有字母n表示的∠3的度数,有已知条件n∠3=2700°,解方程即可求得未知数m,即顶点的个数.
解答 解:如图,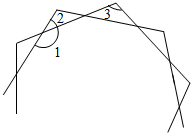
假设有n个点,为方便计算,假设它们均匀分布
则内部构成一个正n边形
因为∠1=180°-$\frac{360°}{n}$
所以∠2=$\frac{360°}{n}$
所以∠3=180°-2∠2=180°-$\frac{720°}{n}$
所以n∠3=n180°-720°
由题意可知n∠3=2700°
即n180°-720°=2700°
n180°-720°+720°=2700°+720°
n180°=3420°
n180°÷180°=3420°÷180°
n=19
答:圆周上有19个点.
点评 此题属于奥数类题型,对一般学生来说,难度较大.关键弄清分别连结1、3、5,2、4、6…通过连结,这些点的个数在内部形成一个与点的个数相同的多边形,再根据多边形每个内角的度数及已知条件解答.

练习册系列答案
相关题目
4.下面属于循环小数的是( )
| A. | O.21414 | B. | 12.32424… | C. | 6.030030003… |
19.春兰小学三年级全体同学去参观博物馆,下面是品年级各班的人数统计表,可是有两个数字看不清了.每人一张门票,王老师已经买好了门票.王老师可能买了( )张门票.
| 班级 | 三(1) | 三(2) | 三(3) | 三(4) | 三(5) | 三(6) |
| 人数 | 42 | 41 | 4? | 4? | 45 | 40 |
| A. | 238 | B. | 245 | C. | 253 | D. | 300 |