题目内容
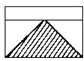 如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为
如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为| 8 |
| 3 |
| 8 |
| 3 |
分析:根据“阴影三角形面积为1平方厘米,”知道长方形的长与三角形的高的关系,再根据“两个长方形的宽的比为1:3,”可以知道大长方形的宽,而此时原长方形的长和宽也可以表示出来,由此列式解答即可.
解答:解:设一长方形被一条直线分成两个长方形的宽分别是a和b,则a:b=1:3,
b=3a,大长方形的宽是a+b=
b+b=
b,
设长方形的长是c,则cb×
=1,
所以cb=2(平方厘米),
原长方形的面积是:c×(a+b)=c×
b=
bc=
×2=
(平方厘米);
故答案为:
.
b=3a,大长方形的宽是a+b=
| 1 |
| 3 |
| 4 |
| 3 |
设长方形的长是c,则cb×
| 1 |
| 2 |
所以cb=2(平方厘米),
原长方形的面积是:c×(a+b)=c×
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:解答此题关键是弄清题意,根据各个图形之间的联系,确定计算方法,列式解答即可.

练习册系列答案
相关题目
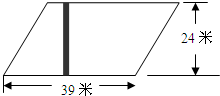 一块近似平行四边形的桃园,被一条长方形的石子路分成了两块(如图).已知平行四边形的底是39米,高是24米,小路宽1米.如果平均每棵桃树占地5平方米,这个桃园大约有多少棵桃树?
一块近似平行四边形的桃园,被一条长方形的石子路分成了两块(如图).已知平行四边形的底是39米,高是24米,小路宽1米.如果平均每棵桃树占地5平方米,这个桃园大约有多少棵桃树?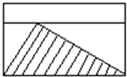 一个长方形被一条直线分成两个长方形,这两个长方形的宽的比是1:2(如图),假设图中阴影部分的面积为4平方厘米,原来长方形的面积是多少?
一个长方形被一条直线分成两个长方形,这两个长方形的宽的比是1:2(如图),假设图中阴影部分的面积为4平方厘米,原来长方形的面积是多少?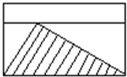 一个长方形被一条直线分成两个长方形,这两个长方形的宽的比是1:2(如图),假设图中阴影部分的面积为4平方厘米,原来长方形的面积是多少?
一个长方形被一条直线分成两个长方形,这两个长方形的宽的比是1:2(如图),假设图中阴影部分的面积为4平方厘米,原来长方形的面积是多少?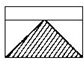 如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为________平方厘米.
如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1:3,若阴影三角形面积为1平方厘米,则原长方形面积为________平方厘米.