题目内容
如图1,长为20厘米、宽为2厘米的长方形沿箭头方向以一定的速度从正方形的左边运行到右边,图2是运行过程中长方形和正方形的重叠面积与运行时间关系图的一部分.

(1)运行8秒后,重叠面积是
(2)正方形的边长是
(3)长方形运行的速度是每秒
(4)若重叠面积为16平方厘米,则长方形运行的时间为

(1)运行8秒后,重叠面积是
24
24
平方厘米;(2)正方形的边长是
12
12
厘米;(3)长方形运行的速度是每秒
2
2
厘米;(4)若重叠面积为16平方厘米,则长方形运行的时间为
4秒或14秒
4秒或14秒
.分析:(1)从折线统计图中读出运行8秒后的面积即可;
(2)从上边给出的图中,可以看出运行6秒后,重叠部分的面积不再发生变化,从而知道6秒时长方形和正方形的位置关系,6×2=12厘米,这个正方形的边长是12厘米.
(3)正方形的边长是12厘米,那么也就是长方形6秒钟运行的路程,用这个路程除以6秒就是它的速度;
(4)分为2种情况:一是长方形的前头,还没有完全穿过正方形,用16平方厘米除以2厘米,求出此时重叠部分长方形的长,再除以它的速度,就是需要的时间;
二是长方形的后头已经进入正方形,此时长方形已经走的路程就是20厘米加上重叠部分长方形的长,再用这个路程除以速度就是运行的时间.
(2)从上边给出的图中,可以看出运行6秒后,重叠部分的面积不再发生变化,从而知道6秒时长方形和正方形的位置关系,6×2=12厘米,这个正方形的边长是12厘米.
(3)正方形的边长是12厘米,那么也就是长方形6秒钟运行的路程,用这个路程除以6秒就是它的速度;
(4)分为2种情况:一是长方形的前头,还没有完全穿过正方形,用16平方厘米除以2厘米,求出此时重叠部分长方形的长,再除以它的速度,就是需要的时间;
二是长方形的后头已经进入正方形,此时长方形已经走的路程就是20厘米加上重叠部分长方形的长,再用这个路程除以速度就是运行的时间.
解答:解:(1)从折线统计图可以看出:运行8秒后,重叠面积是 24平方厘米;
(2)6×2=12(厘米);
答:正方形的边长是 12厘米.
(3)12÷6=2(厘米/秒);
答:长方形运行的速度是每秒 2厘米.
(4)第一种情况:
16÷2=8(厘米);
8÷2=4(秒);
第二种情况:
(20+8)÷2,
=28÷2,
=14(秒);
答:长方形运行的时间为4秒或14秒.
故答案为:24,12,2,4秒或14秒.
(2)6×2=12(厘米);
答:正方形的边长是 12厘米.
(3)12÷6=2(厘米/秒);
答:长方形运行的速度是每秒 2厘米.
(4)第一种情况:
16÷2=8(厘米);
8÷2=4(秒);
第二种情况:
(20+8)÷2,
=28÷2,
=14(秒);
答:长方形运行的时间为4秒或14秒.
故答案为:24,12,2,4秒或14秒.
点评:此题综合性较强,综合考查了匀速运动这一知识,以及分析折线统计图的能力.

练习册系列答案
相关题目
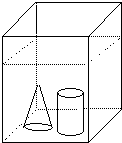 (2011?郑州模拟)如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
(2011?郑州模拟)如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
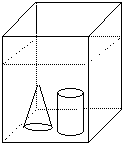 如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?