题目内容
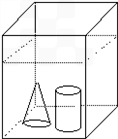
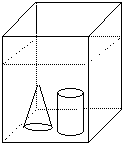 如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
解:上升部分水的体积即圆柱与圆锥的体积之和是:2
0×12×1=240(立方厘米),
因为等底等高的圆柱的体积:圆锥的体积=3:1,
3+1=4,
所以圆柱的体积为:240× =180(立方厘米),
=180(立方厘米),
圆锥的体积为:240× =60(立方厘米),
=60(立方厘米),
答:圆柱的体积是180立方厘米,圆柱的体积是60立方厘米.
分析:根据题干分析可得:这个圆柱和圆锥的体积,就等于这个长方体的容器中上面上升1厘米的水体积,由此利用长方体的体积公式求得上升部分水的体积,即这个圆柱与圆锥的体积之和;因为等底等高的圆柱是圆锥的体积的3倍,把它们的体积之和平均分成四份,那么圆锥的体积就是其中的1份,圆柱的体积是占其中的3份,由此即可解决问题.
点评:此题考查了等底等高的圆柱和圆锥的体积倍数关系的灵活应用;根据题干得出上升部分水的体积就是这两个立体图形的体积之和是解决本题的关键.
0×12×1=240(立方厘米),
因为等底等高的圆柱的体积:圆锥的体积=3:1,
3+1=4,
所以圆柱的体积为:240×
 =180(立方厘米),
=180(立方厘米),圆锥的体积为:240×
 =60(立方厘米),
=60(立方厘米),答:圆柱的体积是180立方厘米,圆柱的体积是60立方厘米.
分析:根据题干分析可得:这个圆柱和圆锥的体积,就等于这个长方体的容器中上面上升1厘米的水体积,由此利用长方体的体积公式求得上升部分水的体积,即这个圆柱与圆锥的体积之和;因为等底等高的圆柱是圆锥的体积的3倍,把它们的体积之和平均分成四份,那么圆锥的体积就是其中的1份,圆柱的体积是占其中的3份,由此即可解决问题.
点评:此题考查了等底等高的圆柱和圆锥的体积倍数关系的灵活应用;根据题干得出上升部分水的体积就是这两个立体图形的体积之和是解决本题的关键.

练习册系列答案
相关题目
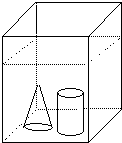 (2011?郑州模拟)如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少?
(2011?郑州模拟)如图:在长方体容器内装有水,已知容器内壁底面长为20厘米,宽为12厘米,现把一小圆柱体和一小圆锥体浸没于水中,水面上升了1厘米.如果圆锥和圆柱的底面积相等,高也相等,求圆柱和圆锥的体积各是多少? 如图,在长方体容器内装有水,已知容器的内壁底面长方形的长为14厘米,宽为9厘米,现在把一个圆柱体和一个圆锥体放入容器内,水面就升高2厘米,又已知放入容器后,圆锥体和圆柱体全部浸没于水中,如果圆柱体和圆锥体的底面半径和高都分别相等,求圆柱体的体积及圆锥体的体积.
如图,在长方体容器内装有水,已知容器的内壁底面长方形的长为14厘米,宽为9厘米,现在把一个圆柱体和一个圆锥体放入容器内,水面就升高2厘米,又已知放入容器后,圆锥体和圆柱体全部浸没于水中,如果圆柱体和圆锥体的底面半径和高都分别相等,求圆柱体的体积及圆锥体的体积.