题目内容
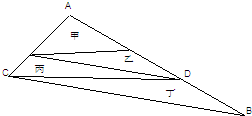在下图三角形ABC中的甲、乙、丙、丁四个小三角形的面积相等．AB长3.6厘米，DB长是0.9
0.9
厘米．分析：由题意和图可知△ACD和△CDB高相等，根据高一定，面积和底成正比，所以S△ACD：S△CDB=（甲的面积+乙的面积+丙的面积）：丁=3：1，进而可求出DB的长．
解答：解：根据高一定，面积和底成正比可知：
S△ACD：S△CDB=（甲的面积+乙的面积+丙的面积）：丁的面积=3：1，
所以AD：DB=3：1，
AB=3.6，
DB=3.6÷（3+1）=0.9，
故答案为：0.9．
S△ACD：S△CDB=（甲的面积+乙的面积+丙的面积）：丁的面积=3：1，
所以AD：DB=3：1，
AB=3.6，
DB=3.6÷（3+1）=0.9，
故答案为：0.9．
点评：解此题的关键是在同一底上，高相等，然后根据高一定，面积和底成正比算出答案．
练习册系列答案
相关题目
在三角形ABC中，点E是BC边上的中点，点F是中线AE上的点，其中AE=3AF，并且延长BF与AC相交于D，如下图所示．若三角形ABC的面积为48，请问三角形AFD的面积是
