Question

求图形阴影部分的面积

Answer 1

解：（1）20×30-20×（30-14）÷2，
=600-160，
=440，
答：阴影部分的面积是440．

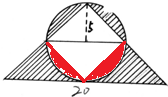
（2）根据题干分析可得，20×5÷2=50，
答：阴影部分的面积是50．

（3）（3+3+5）×4÷2，
=11×2，
=22，
答：阴影部分的面积是22．
分析：（1）观察图形可知，阴影部分的面积等于底是20，高是30的平行四边形的面积与底是20，高是30-14=16的三角形的面积之差，据此计算即可；
（2）如图，上部的两个阴影部分的面积正好等于下面红色部分的面积，则阴影部分的面积就等于底为20，高为5的三角形的面积，据此计算即可；

（3）观察图形可知，阴影部分是一个梯形，上底是3，下底是3+5=8，高是4，据此利用梯形的面积公式计算即可解答．
点评：此题主要考查组合图形的面积的计算方法，利用等积变形转化不规则图形的面积是解决此类问题的关键．