题目内容
2.作图.
(1)先画一个直径4cm的圆,再在这个圆里画一个最大的正方形
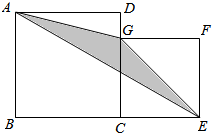
(2)求阴影部分的面积.
分析 (1)圆心确定圆的位置,半径确定圆的大小,由此以任意一点O为圆心,以4÷2=2厘米为半径画圆即可;圆内最大的正方形的对角线即为圆的直径,先画出两条互相垂直的直径,再连接直径与圆的交点,即为圆里最大的正方形;
(2)用长方形的面积减去半圆的面积就是阴影部分的面积,长方形的宽就是圆的半径,根据长方形和圆的面积公式解答即可.
解答 解:(1)根据分析画图如下: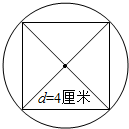
(2)10×(10÷2)-3.14×(10÷2)2÷2
=10×5-3.14×25÷2
=50-39.25
=10.75(米2),
答:阴影部分的面积是10.75米2.
点评 (1)此题考查了圆的画法以及画出圆内最大的正方形,关键是明确圆内最大的正方形的特点是:两条对角线正好是圆的两条互相垂直的直径;(2)本题属于求组合图形面积的问题,这种类型的题目主要明确组合图形是由哪些基本的图形构成的,然后看是求几种图形的面积和还是求面积差,然后根据面积公式解答即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下面是三年级两个班部分学生参加课外兴趣小组的情况统计表.
(1)三年级两个班参加计算机组的人最多,有30人.
(2)三年级两个班参加篮球组组的人最少,比参加人数最多的组少17人.
(3)(1)班参加兴趣小组的共有40人,与(2)班参加兴趣小组的总人数相差2人.
| 兴趣组、人数、班级 | 篮球组 | 舞蹈组 | 计算机组 | 长跑组 |
| (1)班 | 6 | 8 | 15 | 11 |
| (2)班 | 7 | 10 | 15 | 10 |
(2)三年级两个班参加篮球组组的人最少,比参加人数最多的组少17人.
(3)(1)班参加兴趣小组的共有40人,与(2)班参加兴趣小组的总人数相差2人.