题目内容
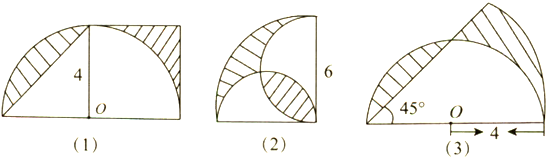
求各图形中阴影部分的面积.(单位:厘米)


分析:(1)观察图形可知,S阴影=
S正方形+
S圆-2S扇形,利用相关公式代入数值求解即可;
(2)观察图形可知,阴影部分的面积等于扇形的面积加上梯形的面积减去三角形的面积,利用相关公式代入数值求解即可;
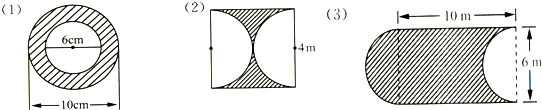
(3)观察图形可知,阴影部分的面积等于小圆的面积;
(4)阴影部分的面积等于图中4个扇形的面积之和;
(5)连结GF,如下图,

可知,阴影部分的面积等于梯形ACDB的面积加上正方形CEFD的面积减去三角形GEF和三角形GHF的面积.
| 3 |
| 2 |
| 1 |
| 2 |
(2)观察图形可知,阴影部分的面积等于扇形的面积加上梯形的面积减去三角形的面积,利用相关公式代入数值求解即可;
(3)观察图形可知,阴影部分的面积等于小圆的面积;
(4)阴影部分的面积等于图中4个扇形的面积之和;
(5)连结GF,如下图,

可知,阴影部分的面积等于梯形ACDB的面积加上正方形CEFD的面积减去三角形GEF和三角形GHF的面积.
解答:解:(1)S阴影=
S正方形+
S圆-2S扇形=
×20×20+
×π×(
)2-2×
×π×202
=600+50π-200π
=600-150π
=600-150×3.14
=600-471
=129(平方厘米);
答:阴影部分的面积是129平方厘米;
(2)S阴影=S扇形+S梯形-S三角形=
×3.14×62+(6+4)×4×
-(6+4)×4×
=28.26(平方厘米);
答:阴影部分的面积是28.26平方厘米;
(3)S阴影=S小圆=3.14×(
)2=78.5(平方厘米);
答:阴影部分的面积是78.5平方厘米;
(4)S阴影=
π×[12+(1+1)2+(1+1+1)2+(1+1+1+1)2]=
π×30=23.55(平方厘米);
答:阴影部分的面积是23.55平方厘米;
(5)S阴影=(3+3+4)×2×
+4×4-4×(4+2)×
-(4-1)×
×
=11(平方厘米).
答:阴影部分的面积是11平方厘米.
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 20 |
| 2 |
| 90 |
| 360 |
=600+50π-200π
=600-150π
=600-150×3.14
=600-471
=129(平方厘米);
答:阴影部分的面积是129平方厘米;
(2)S阴影=S扇形+S梯形-S三角形=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
答:阴影部分的面积是28.26平方厘米;
(3)S阴影=S小圆=3.14×(
| 20 |
| 4 |
答:阴影部分的面积是78.5平方厘米;
(4)S阴影=
| 1 |
| 4 |
| 1 |
| 4 |
答:阴影部分的面积是23.55平方厘米;
(5)S阴影=(3+3+4)×2×
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 2 |
| 1 |
| 2 |
答:阴影部分的面积是11平方厘米.
点评:本题考查了组合图形的面积,较为复杂,关键还是把不规则图形的面积转化为规则图形的面积的和与差,再利用公式即可解决.

练习册系列答案
相关题目