题目内容
 如图,已知长方形ABCD的面积是24平方厘米,三角形ABE的面积是5平方厘米,三角形AFD的面积是6平方厘米,那么三角形AEF的面积是________平方厘米.
如图,已知长方形ABCD的面积是24平方厘米,三角形ABE的面积是5平方厘米,三角形AFD的面积是6平方厘米,那么三角形AEF的面积是________平方厘米.
9.5
分析:连接长方形对角线AC,通过S△AFD和S△ACF来判定F是DC边的中点,然后通过S△ABE和S△AEC,来判定BE:EC=5:7,从而求出S△EFC的面积,最后用长方形的面积减去S△ABE,S△ADF和S△CEF的面积即可.
解答:连接长方形对角线AC,如下图:

可知S△ABC=S△ACD=12(平方厘米),
因为S△AFD=6(平方厘米),所以S△ACF=6(平方厘米),由此可知F是DC边的中点,
因为S△ABE=5(平方厘米),所以S△AEC=7(平方厘米),由此可知BE:EC=5:7,
S△EFC= ×CF×CE=3.5(平方厘米),
×CF×CE=3.5(平方厘米),
S△AEF=S长-S△ABE-S△ADF-S△CEF,
=24-5-6-3.5,
=9.5(平方厘米);
故答案为:9.5.
点评:此题考查了求组合图形的面积.
分析:连接长方形对角线AC,通过S△AFD和S△ACF来判定F是DC边的中点,然后通过S△ABE和S△AEC,来判定BE:EC=5:7,从而求出S△EFC的面积,最后用长方形的面积减去S△ABE,S△ADF和S△CEF的面积即可.
解答:连接长方形对角线AC,如下图:

可知S△ABC=S△ACD=12(平方厘米),
因为S△AFD=6(平方厘米),所以S△ACF=6(平方厘米),由此可知F是DC边的中点,
因为S△ABE=5(平方厘米),所以S△AEC=7(平方厘米),由此可知BE:EC=5:7,
S△EFC=
 ×CF×CE=3.5(平方厘米),
×CF×CE=3.5(平方厘米),S△AEF=S长-S△ABE-S△ADF-S△CEF,
=24-5-6-3.5,
=9.5(平方厘米);
故答案为:9.5.
点评:此题考查了求组合图形的面积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图. 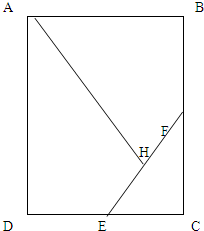 如图,在长方形ABCD中,已知E是DC的中点,F是BC的中点,H是FE的中点,AB=12分米,BC=20分米,那么三角形AHE的面积是多少?(提示:连接AE、AF)
如图,在长方形ABCD中,已知E是DC的中点,F是BC的中点,H是FE的中点,AB=12分米,BC=20分米,那么三角形AHE的面积是多少?(提示:连接AE、AF)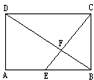 如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.
如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.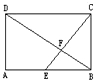 如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积.
如图,E是长方形ABCD边AB的中点,已知三角形EBF的面积是1cm2,求长方形ABCD的面积. 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图.