题目内容
8.解方程.30x+15x-0.5=22; 0.25(2÷x)=2.5; 712-a+13=1.
分析 (1)先根据乘法分配律将原方程化简,再根据等式的性质,在方程两边先同时加上0.5,再同时除以45,即可得解.
(2)根据等式的性质,在方程两边先同时除以0.25,再同时乘以x,最后再同时除以10,即可得解.
(3)先将原方程化简,再根据等式的性质,在方程两边先同时加a,再同时减去1,即可得解.
解答 解:
(1)30x+15x-0.5=22
(30+15)x-0.5=22
45x-0.5=22
45x-0.5+0.5=22+0.5
45x=22.5
45x÷45=22.5÷45
x=0.5
(2)0.25(2÷x)=2.5
0.25(2÷x)÷0.25=2.5÷0.25
2÷x=10
2÷x×x=10×x
2=10x
2÷10=10x÷10
0.2=x
x=0.2
(3)712-a+13=1
712-a+412=1
1112-a=1
1112-a+a=1+a
1112=1+a
1112-1=1+a-1
a=-112
点评 此题考查了根据等式的性质解方程,即等式两边同加上、同减去、同乘上或同除以一个不为0的数,等式仍相等.同时注意“=”上下要对齐.

练习册系列答案
相关题目
13.直接写出得数.
| 17-19= | 1-215= | 0.25×0.1= | 0.8÷0.01= | 2-713= |
| 1-0.01= | 3+45= | 25+23-25= | 29+45+79+15= | 58-(58-12)= |
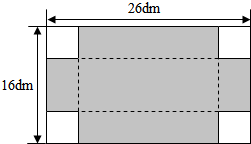 一块长方形的铁皮,如图,从四个角剪掉边长为3分米的正方形,然后沿图中的虚线向上折,焊接成一个无盖的盒子.这个盒子用了多少铁皮?(不包括剪掉的部分)它的容积是多少?
一块长方形的铁皮,如图,从四个角剪掉边长为3分米的正方形,然后沿图中的虚线向上折,焊接成一个无盖的盒子.这个盒子用了多少铁皮?(不包括剪掉的部分)它的容积是多少?