Question

12．图A是棱长为1立方厘米的小正方体，图B、图C由这样的小正方体摆放而成．按照这样的方法继续摆放，自上而下分别叫第一层、第二层…第n层小正方体的个数为$\frac{n（n+1）}{2}$（用含n的式子表示）．当层数为10时，这堆小正方体的总个数为55．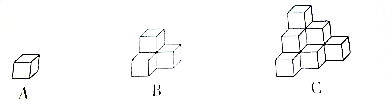

Answer 1

分析 （1）图（1）有1层，共1个小正方体，图（2）有2层，第2层正方体的个数为1+2…根据相应规律可得第n
层正方体的个数；
（2）依据（1）得到的规律可得当n=10时，正方体的个数．

解答 解：（1）图A有1层，共1个小正方体，
图B有2层，第2层正方体的个数为1+2；
图C有3层，第3层正方体的个数为：1+2+3=6；
第n层小正方体的个数为1+2+3+4+5+6+…+n=$\frac{n（n+1）}{2}$．
（2）当n=10时，s=1+2+3+4+5+6+…+10=55．
故答案为$\frac{n（n+10）}{2}$；55．

点评 此题主要考查了图形的变化规律，根据图形得出第n层为：s=1+2+…+n=$\frac{n（n+1）}{2}$是解决问题的关键．