题目内容
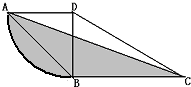 图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米?
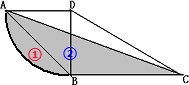
图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米?分析:如图所示,将阴影分为①、②两部分,阴影①的面积=以4厘米为半径的
圆的面积-三角形ABD的面积,阴影②的面积=三角形ABC的面积,三角形ABC的底BC的长度已知,其高就为DB,且其长度为4厘米,于是即可利用三角形和圆的面积公式即可求解.
| 1 |
| 4 |

解答:解:
×3.14×42-4×4÷2+6×4÷2,
=12.56-8+12,
=4.56+12,
=16.56(平方厘米);
答:阴影部分的面积是16.56平方厘米.
| 1 |
| 4 |
=12.56-8+12,
=4.56+12,
=16.56(平方厘米);
答:阴影部分的面积是16.56平方厘米.
点评:解答此题的关键是:将阴影部分分成两部分,分别计算即可求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
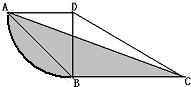 图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米?
图中三角形ABD是一个等腰直角三角形,弧AB为四分之一圆弧,AD的长为4厘米,BC的长为6厘米,阴影部分的面积是多少平方厘米?