题目内容
13名乒乓球运动员分成三队,进行单打比赛.规定同队的运动员彼此之间不比赛,不同队的运动员两两比赛一场,那么比赛的总场数最少是 场,最多是 场.
考点:排列组合
专题:传统应用题专题
分析:(1)如果要使比赛的总场数最少,那么根据“同队的运动员彼此之间不比赛,”可知,必须使其中一个队的人数尽量最多,并且差最大,因为:13=1+1+11,所以分成三队是:第一队1人,第二队1人,第三队11人,因此根据排列组合知识可得比赛的总场数最少是:1×11+1×11+1×1=23(场);
(2)同理,如果要使比赛的总场数最多,那么根据“同队的运动员彼此之间不比赛,”可知,三个队的人数应尽量接近,因为:13=5+4+4,所以分成三队是:第一队5人,第二队4人,第三队4人,因此根据排列组合知识可得比赛的总场数最多是:5×4+5×4+4×4=56(场);据此解答.
(2)同理,如果要使比赛的总场数最多,那么根据“同队的运动员彼此之间不比赛,”可知,三个队的人数应尽量接近,因为:13=5+4+4,所以分成三队是:第一队5人,第二队4人,第三队4人,因此根据排列组合知识可得比赛的总场数最多是:5×4+5×4+4×4=56(场);据此解答.
解答:
解:(1),因为:13=1+1+11,
所以分成三队是:第一队1人,第二队1人,第三队11人,
因此根据排列组合知识可得比赛的总场数最少是:1×11+1×11+1×1=23(场);
(2)因为:13=5+4+4,
所以分成三队是:第一队5人,第二队4人,第三队4人,
因此根据排列组合知识可得比赛的总场数最多是:5×4+5×4+4×4=56(场);
答:比赛的总场数最少是23场,最多是56场.
故答案为:23,56.
所以分成三队是:第一队1人,第二队1人,第三队11人,
因此根据排列组合知识可得比赛的总场数最少是:1×11+1×11+1×1=23(场);
(2)因为:13=5+4+4,
所以分成三队是:第一队5人,第二队4人,第三队4人,
因此根据排列组合知识可得比赛的总场数最多是:5×4+5×4+4×4=56(场);
答:比赛的总场数最少是23场,最多是56场.
故答案为:23,56.
点评:本题考查了整数的裂项与拆分以及加法原理的综合应用,关键是根据“极值问题”确定两种极值分组,然后把每种分组根据加法原理,再采用科学分类计数原理把每种情况又分三类完成排列.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果甲数的
大于乙数的
,那么甲数和乙数的大小关系是( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、甲>乙 | B、甲=乙 | C、甲<乙 |
用四根木条钉一个长方形,用两手拉住它的对角,向相反方向拉,可以拉成不同的平行四边形,平行四边形的周长( )长方形的周长.
| A、小于 | B、大于 |
| C、等于 | D、不能比较 |
65×4×25=65×(4×25)应用了( )
| A、乘法结合律 | B、乘法交换律 |
| C、乘法分配律 |
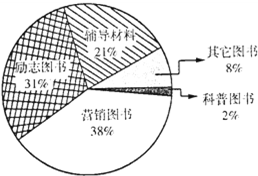 如图是某书店去年销售几种书籍类别的统计图.
如图是某书店去年销售几种书籍类别的统计图.