题目内容
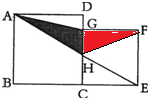
 如图,已知正方形ABCD的边长是6厘米,正方形BEFG的边长是4厘米,阴影部分的面积是
如图,已知正方形ABCD的边长是6厘米,正方形BEFG的边长是4厘米,阴影部分的面积是4.8
4.8
平方厘米.分析:连接HF,根据题意,阴影部分和涂色部分的面积之和,等于两个正方形的面积减去三角形ABE的面积减去三角形EFH的面积再减去三角形ADG的面积,可根据正方形的面积公式和三角形的面积公式进行计算即可得到答案,因为阴影部分与涂色部分的三角形同底,所以面积之比等于它们的高的比,由此按照比的意义即可解答问题.

解答:解:(6×6+4×4)-(4+6)×6÷2-4×4÷2-(6-4)×6÷2,
=(36+16)-10×6÷2-8-2×6÷2,
=52-30-8-6,
=8(平方厘米);
阴影部分的三角形的高是AD=6厘米,涂色部分的三角形的高是GH=4厘米,
所以它们的面积之比是6:4=3:2,
则阴影部分的面积与它们的面积之和的比是3:5,
所以阴影部分的面积是:8×
=4.8(平方厘米),
答:阴影部分的面积是4.8平方厘米.
故答案为:4.8.
=(36+16)-10×6÷2-8-2×6÷2,
=52-30-8-6,
=8(平方厘米);
阴影部分的三角形的高是AD=6厘米,涂色部分的三角形的高是GH=4厘米,
所以它们的面积之比是6:4=3:2,
则阴影部分的面积与它们的面积之和的比是3:5,
所以阴影部分的面积是:8×
| 3 |
| 5 |
答:阴影部分的面积是4.8平方厘米.
故答案为:4.8.
点评:此题主要考查的是三角形的面积公式和长方形的面积公式的应用,以及底一定时,三角形的面积与高成正比例的性质的灵活应用.

练习册系列答案
相关题目
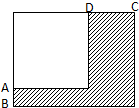 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图.  在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米?
在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米? 如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长.
如图,已知正方形ABCD的边长为10,若以A为圆心,10为半径,画扇形ABD;在扇形ABD内作⊙O与AD、AB、弧都相切,求⊙O的周长.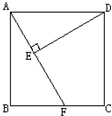 在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米?
在正方形ABCD中,如图,已知AB=4厘米,AF=5厘米,则DE的长是多少厘米? 一个长方形的纸剪去一个正方形后,剩下如图.
一个长方形的纸剪去一个正方形后,剩下如图.