题目内容
1.加工一批零件,单独做,师傅5天完成$\frac{1}{3}$,徒弟4天完成$\frac{1}{5}$,两人合作,一天完成这批零件的$\frac{()}{()}$,6天完成这批零件的$\frac{7}{10}$.分析 首先根据工作效率=工作量÷工作时间,分别求出师徒两人的工作效率各是多少;然后把两人的工作效率求和,求出两人合作,一天完成这批零件的几分之几;最后根据工作时间=工作量÷工作效率,求出多少天完成这批零件的$\frac{7}{10}$即可.
解答 解:$\frac{1}{3}÷5+\frac{1}{5}÷4$
=$\frac{1}{15}+\frac{1}{20}$
=$\frac{7}{60}$
$\frac{7}{10}÷\frac{7}{60}=6(天)$
答:一天完成这批零件的$\frac{7}{60}$,6天完成这批零件的$\frac{7}{10}$.
故答案为:$\frac{7}{60}、6$.
点评 此题主要考查了工程问题的应用,对此类问题要注意把握住基本关系,即:工作量=工作效率×工作时间,工作效率=工作量÷工作时间,工作时间=工作量÷工作效率,解答此题的关键是求出师徒两人的工作效率各是多少.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
3.脱式计算,能简算的要简算.
| ($\frac{5}{6}$-$\frac{5}{9}$)×$\frac{18}{5}$ | $\frac{6}{13}$×$\frac{7}{5}$-$\frac{6}{13}$×$\frac{2}{5}$ | $\frac{4}{5}$÷[($\frac{3}{5}$+$\frac{1}{2}$)×2] |
| 34×$\frac{34}{35}$ | 1-$\frac{5}{8}$÷$\frac{25}{28}$-$\frac{3}{10}$ | $\frac{3}{5}$×99+$\frac{3}{5}$ |
11.
| 7t=7000kg | 5kg=5000g | 2t=2000kg |
| 3000kg=3t | 1吨=1000千克 | 9000g=9kg |
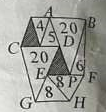 如图,AB,CD,EF,GH两两平行且AB=CD=EF=GH,图中每个数字表示其所在三角形的面积,图中两个阴影三角形的面积和是多少?
如图,AB,CD,EF,GH两两平行且AB=CD=EF=GH,图中每个数字表示其所在三角形的面积,图中两个阴影三角形的面积和是多少?