题目内容
 如图所示的梯形ABCD中,E是AD边上的中点,直线CE把梯形ABCD分成甲、乙两部分,它们的面积比是10:7,上底AB与下底CD的比是________.
如图所示的梯形ABCD中,E是AD边上的中点,直线CE把梯形ABCD分成甲、乙两部分,它们的面积比是10:7,上底AB与下底CD的比是________.
3:14
分析:先连接AC,E是AD中点,那么△ACE的面积=△乙的面积,可知△ABC的面积=△甲的面积-△ACE的面积=△甲的面积-△乙的面积,又已知S△甲:S△乙=10:7,可以把S△甲的面积看作10,S△乙的面积看作7,所以即可救出S△ABC,
又因为AB∥CD,所以△ABC与△ACD是等高不等底的,高一定时,三角形的面积与底成正比的关系可得出:AB:CD=S△ABC:S△ACD,解出即可.
解答:先连接AC,E是AD中点,
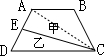
那么△ACE=△乙,
又已知S△甲:S△乙=10:7,可以把S△甲的面积看作10,S△乙的面积看作7,
又因为S△ABC=S△甲-S△ACE
=10-7,
=3,
又因为AB∥CD,
所以△ABC与△ACD是等高不等底的,
高一定时,三角形的面积与底成正比的关系可得出:
AB:CD=△ABC的面积:△ACD的面积,
AB:CD=3:(7+7),
AB:CD=3:14,
答:梯形的上底AB与下底CD的长度比AB:CD=3:14.
故答案为:3:14.
点评:此题考查了两个三角形等底等高时,面积相等;高一定时,三角形的面积与底成正比的关系的灵活应用.
分析:先连接AC,E是AD中点,那么△ACE的面积=△乙的面积,可知△ABC的面积=△甲的面积-△ACE的面积=△甲的面积-△乙的面积,又已知S△甲:S△乙=10:7,可以把S△甲的面积看作10,S△乙的面积看作7,所以即可救出S△ABC,
又因为AB∥CD,所以△ABC与△ACD是等高不等底的,高一定时,三角形的面积与底成正比的关系可得出:AB:CD=S△ABC:S△ACD,解出即可.
解答:先连接AC,E是AD中点,

那么△ACE=△乙,
又已知S△甲:S△乙=10:7,可以把S△甲的面积看作10,S△乙的面积看作7,
又因为S△ABC=S△甲-S△ACE
=10-7,
=3,
又因为AB∥CD,
所以△ABC与△ACD是等高不等底的,
高一定时,三角形的面积与底成正比的关系可得出:
AB:CD=△ABC的面积:△ACD的面积,
AB:CD=3:(7+7),
AB:CD=3:14,
答:梯形的上底AB与下底CD的长度比AB:CD=3:14.
故答案为:3:14.
点评:此题考查了两个三角形等底等高时,面积相等;高一定时,三角形的面积与底成正比的关系的灵活应用.

练习册系列答案
相关题目
 如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的
如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的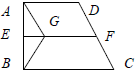 如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的
如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的 ,那么EG的长是几厘米?
,那么EG的长是几厘米?