题目内容
 如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的
如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的| 1 | 5 |
分析:因为EF是梯形ABCD的中位线,所以EF=(AD+BC)÷2,即AD+BC=15×2,再根据梯形的面积公式S=(a+b)×h÷2,得出梯形ABCD的面积为(AD+BC)×AB÷2;由三角形的面积公式S=ab÷2,知道三角形ABG的面积是AB×EG÷2,再由三角形ABG的面积是梯形ABCD面积的
,列出等式解答即可.
| 1 |
| 5 |
解答:解:因为EF是梯形ABCD的中位线,所以AD+BC=15×2=30(厘米),
梯形ABCD的面积为:
(AD+BC)×AB÷2=30×AB÷2,
三角形ABG的面积是:
AB×EG÷2,
所以AB×EG÷2=
×30×AB÷2,
即EG=6厘米;
答:EG的长是6厘米.
梯形ABCD的面积为:
(AD+BC)×AB÷2=30×AB÷2,
三角形ABG的面积是:
AB×EG÷2,
所以AB×EG÷2=
| 1 |
| 5 |
即EG=6厘米;
答:EG的长是6厘米.
点评:解答本题的关键是利用三角形的面积公式与梯形的面积公式表示出图中的梯形和三角形的面积,再由“三角形ABG的面积是梯形ABCD面积的
,”列出等式解答即可.
| 1 |
| 5 |

练习册系列答案
相关题目
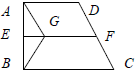 如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的
如图所示,梯形ABCD的中位线EF长15厘米,∠ABC=∠AEF=90°,G是EF上的一点.如果三角形ABG的面积是梯形ABCD面积的 ,那么EG的长是几厘米?
,那么EG的长是几厘米?