题目内容
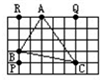如图，每个小方格的面积是1cm2，那么△ABC的面积是________cm2．
8.5
分析：△ABC的面积为长方形RPCQ的面积减三角形ARB的面积减三角形BPC的面积再减三角形CQA的面积，将数据代入公式即可求解．
解答：如图所示，
S△ARB=
S长方形ARBH=×6=3（平方厘米），
S△BPC=S长方形BPCE=×5=2.5（平方厘米），
S△CQA=S长方形CQAF=×12=6（平方厘米），
则，S△ABC=S长方形-S△ARB-S△BPC-S△CQA，
=20-3-2.5-6，
=8.5（平方厘米）．
故答案为：8.5．
点评：此题主要考查组合图形的面积，关键是将图形进行合理的分割．
分析：△ABC的面积为长方形RPCQ的面积减三角形ARB的面积减三角形BPC的面积再减三角形CQA的面积，将数据代入公式即可求解．
解答：如图所示，
S△ARB=
S长方形ARBH=×6=3（平方厘米），S△BPC=
S长方形BPCE=×5=2.5（平方厘米），S△CQA=
S长方形CQAF=×12=6（平方厘米），则，S△ABC=S长方形-S△ARB-S△BPC-S△CQA，
=20-3-2.5-6，
=8.5（平方厘米）．
故答案为：8.5．
点评：此题主要考查组合图形的面积，关键是将图形进行合理的分割．
练习册系列答案
相关题目
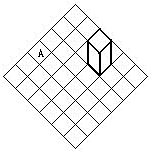如图，在6×6的方格纸上放着一个小立方体，它每个面大小与方格大小相同，现在要翻转小立方体，使其走遍所有的方格，每个方格只能走一次，最后小立方体落到方格A内．问有可能吗？
