题目内容
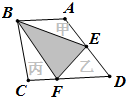 如图,梯形ABCD的面积是35平方厘米,AE=ED,图中三角形甲、乙、丙的面积相等,求阴影部分的面积.
如图,梯形ABCD的面积是35平方厘米,AE=ED,图中三角形甲、乙、丙的面积相等,求阴影部分的面积.
解:因为AE=ED,又因为甲的面积=乙的面积,
所以甲和乙一定等底等高,
所以AD∥BF,
又因为ABCD是梯形,
所以AB∥CD,所以ABFD是平行四边形,
所以阴影的面积=2个乙的面积,
把梯形ABCD的面积分成5份,阴影占2份,
所以阴影的面积=35÷5×2=14(平方厘米).
答:阴影部分的面积是14平方厘米.
分析:因为AE=ED,又因为甲的面积=乙的面积,所以甲和乙一定等底等高,所以AD∥BF又因为ABCD是梯形,所以AB∥CD,所以ABFD是平行四边形,根据等底等高的三角形的面积是平行四边形面积的一半,所以阴影的面积=2个乙的面积,梯形ABCD的面积分成5份,阴影占2份,据此解答即可.
点评:此题考查阴影部分的面积,解决此题的关键是根据已知条件推导出ABFD是平行四边形.
所以甲和乙一定等底等高,
所以AD∥BF,
又因为ABCD是梯形,
所以AB∥CD,所以ABFD是平行四边形,
所以阴影的面积=2个乙的面积,
把梯形ABCD的面积分成5份,阴影占2份,
所以阴影的面积=35÷5×2=14(平方厘米).
答:阴影部分的面积是14平方厘米.
分析:因为AE=ED,又因为甲的面积=乙的面积,所以甲和乙一定等底等高,所以AD∥BF又因为ABCD是梯形,所以AB∥CD,所以ABFD是平行四边形,根据等底等高的三角形的面积是平行四边形面积的一半,所以阴影的面积=2个乙的面积,梯形ABCD的面积分成5份,阴影占2份,据此解答即可.
点评:此题考查阴影部分的面积,解决此题的关键是根据已知条件推导出ABFD是平行四边形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
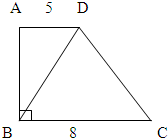 如图,梯形ABCD的上底长5厘米,下底长8厘米,已知三角形DBC的面积是24平方厘米,求梯形的面积.
如图,梯形ABCD的上底长5厘米,下底长8厘米,已知三角形DBC的面积是24平方厘米,求梯形的面积.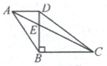 如图,梯形ABCD的上底AD长12厘米,高BD长18厘米,BE=2DE,则下底BC长
如图,梯形ABCD的上底AD长12厘米,高BD长18厘米,BE=2DE,则下底BC长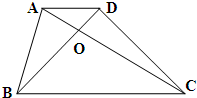 如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米.三角形ABO的面积为12平方厘米,则梯形ABCD的面积为
如图,梯形ABCD的上底AD长为3厘米,下底BC长为9厘米.三角形ABO的面积为12平方厘米,则梯形ABCD的面积为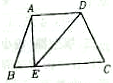 如图,梯形ABCD的面积为20.点E在BC上,三角形ADE的面积是三角形ABE的面积的2倍.BE的长为2,EC
如图,梯形ABCD的面积为20.点E在BC上,三角形ADE的面积是三角形ABE的面积的2倍.BE的长为2,EC 如图直角梯形ABCD的面积为200平方厘米,已知AB=20厘米,DC=5厘米,阴影部分的面积是
如图直角梯形ABCD的面积为200平方厘米,已知AB=20厘米,DC=5厘米,阴影部分的面积是