题目内容
 如图1,三边长分别为5、12、13的直角三角形,把短直角边折叠到长直角边上(图2),求图2中阴影部分的面积.
如图1,三边长分别为5、12、13的直角三角形,把短直角边折叠到长直角边上(图2),求图2中阴影部分的面积.分析:如图所示,因为三角形CDE和三角形ADE是等高不等底的三角形,所以它们的面积比就等于底的比;又因三角形CDE和三角形CBE的面积相等,则CB=CD=5,
CD:DA=5:(13-5)=5:8,S△ADE:S△CDE:S△CBE=8:5:5,把S△ABC看作单位“1”,则阴影三角形的面积S△ABC的
,S△ABC可求,从而可以求得阴影部分的面积.
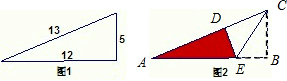
CD:DA=5:(13-5)=5:8,S△ADE:S△CDE:S△CBE=8:5:5,把S△ABC看作单位“1”,则阴影三角形的面积S△ABC的
| 8 |
| 8+5+5 |

解答:解:因为13-5=8,
S△ABC=12×5÷2=30,
所以S阴影=30×
=
;
答:阴影部分的面积是
.
S△ABC=12×5÷2=30,
所以S阴影=30×
| 8 |
| 8+5+5 |
| 40 |
| 3 |
答:阴影部分的面积是
| 40 |
| 3 |
点评:解答此题的关键是:利用等高不等底的三角形面积比就等于底的比,先求得大三角形被分成的总份数,再求阴影部分占总分数的几分之几,从而问题得解.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了
如图,有一个边长为1的正三角形,第一次去掉三边中点连线围成的那个正三角形;第二次对留下的三个正三角形,再分别去掉它们中点连线围成的三角形;…做到第四次后,一共去掉了 如图1,三边长分别为5、12、13的直角三角形,把短直角边折叠到长直角边上(图2),求图2中阴影部分的面积.
如图1,三边长分别为5、12、13的直角三角形,把短直角边折叠到长直角边上(图2),求图2中阴影部分的面积.