题目内容
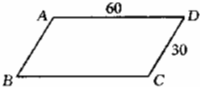 如图,平行四边形的花池边长分别为60米与30米.小明和小华同时从A点出发,沿着平行四边形的边由A→B→C→D→A…顺序走下去.小明每分钟走50米,小华每分钟走20米.出发5分钟后小明走到E点,小华走到F点.连接AE,AF,则四边形AECF的面积与平行四边形ABCD的面积的比是
如图,平行四边形的花池边长分别为60米与30米.小明和小华同时从A点出发,沿着平行四边形的边由A→B→C→D→A…顺序走下去.小明每分钟走50米,小华每分钟走20米.出发5分钟后小明走到E点,小华走到F点.连接AE,AF,则四边形AECF的面积与平行四边形ABCD的面积的比是分析:如图所示,速度和时间已知,于是即可分别求出二人走的路程,从而可以求出EC、CF的长度,则可以求出EC与BC、CF与CD的比,进而得出三角形AEC与三角形ABC、三角形AFC与三角形ACD的面积比,从而得出四边形AECF与ABCD的面积之比.
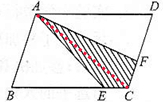

解答:解:50×5=250,
250-(60+30)×2,
=250-180,
=70(米),
所以BE为70-30=40米,
CE为60-40=20米;
20×5=100,
100-(60+30)=10米,
则CF为10米;
所以CE:BC=20:60=1:3,
CF:CD=1:3;
由此可得:S△AEC:S△ABC=S△AFC:S△ACD=1:3,
S△AEC+S△AFC=
(S△ABC+S△ACD)=
S平行四边形ABCD,
即S四边形AECF:S平行四边形ABCD=1:3;
答:四边形AECF与ABCD的面积之比为1:3.
250-(60+30)×2,
=250-180,
=70(米),
所以BE为70-30=40米,
CE为60-40=20米;
20×5=100,
100-(60+30)=10米,
则CF为10米;
所以CE:BC=20:60=1:3,
CF:CD=1:3;
由此可得:S△AEC:S△ABC=S△AFC:S△ACD=1:3,
S△AEC+S△AFC=
| 1 |
| 3 |
| 1 |
| 3 |
即S四边形AECF:S平行四边形ABCD=1:3;
答:四边形AECF与ABCD的面积之比为1:3.
点评:解答此题的关键是先求出二人行走的路程,得出CE、CF的值,进而问题逐步得解.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 解决问题.
解决问题.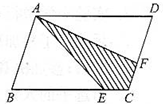 如图,平行四边形花池边长分别为60m和30m,大明与小亮同时从A点出发,逆时针沿平行四边形走,大明每分钟走50米,小亮每分钟走20m,出发5分钟后大明走到E点,小亮走到F点,连接AE、AF,求四边形AECF与ABCD的面积之比.
如图,平行四边形花池边长分别为60m和30m,大明与小亮同时从A点出发,逆时针沿平行四边形走,大明每分钟走50米,小亮每分钟走20m,出发5分钟后大明走到E点,小亮走到F点,连接AE、AF,求四边形AECF与ABCD的面积之比.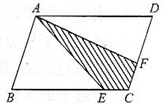 如图,平行四边形花池边长分别为60m和30m,大明与小亮同时从A点出发,逆时针沿平行四边形走,大明每分钟走50米,小亮每分钟走20m,出发5分钟后大明走到E点,小亮走到F点,连接AE、AF,求四边形AECF与ABCD的面积之比.
如图,平行四边形花池边长分别为60m和30m,大明与小亮同时从A点出发,逆时针沿平行四边形走,大明每分钟走50米,小亮每分钟走20m,出发5分钟后大明走到E点,小亮走到F点,连接AE、AF,求四边形AECF与ABCD的面积之比.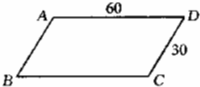 如图,平行四边形的花池边长分别为60米与30米.小明和小华同时从A点出发,沿着平行四边形的边由A→B→C→D→A…顺序走下去.小明每分钟走50米,小华每分钟走20米.出发3分钟后小明走到E点,小华走到F点.连接AE,AF,则四边形AECF的面积与平行四边形ABCD的面积的比是________.
如图,平行四边形的花池边长分别为60米与30米.小明和小华同时从A点出发,沿着平行四边形的边由A→B→C→D→A…顺序走下去.小明每分钟走50米,小华每分钟走20米.出发3分钟后小明走到E点,小华走到F点.连接AE,AF,则四边形AECF的面积与平行四边形ABCD的面积的比是________.