题目内容
把正三角形(等边三角形)每边三等分,将各边的中间段取来向外面作小正三角形,得到一个六角形,再将这个六角形的六个“角”(即小正三角形)的两边三等分,又以它的中间段向外作更小的正三角形,这样就得到下图所示的图形,如果所作的最小三角形的面积为1,求整个图形的面积.
分析:最小的三角形的边长是小三角形的
,根据相似三角形的规律.面积比就是1:9,同理小三角形与最大三角形的面积比也是1:9,而且最小的三角形面积为1.据此就可求出大三角形的面积.
| 1 |
| 3 |
解答:解:由图可知:最小的三角形有12个,面积为12×1=12;
小三角形有3个,面积为3×9=27;
最大的三角形有1个,面积为1×9×9=81;
所以整个图形的面积为:12+27+81=120.

答:整个图形的面积是120.
小三角形有3个,面积为3×9=27;
最大的三角形有1个,面积为1×9×9=81;
所以整个图形的面积为:12+27+81=120.

答:整个图形的面积是120.
点评:此题主要考查等积变形问题,利用边长的特点,先求出面积比,再逐步求总面积.

练习册系列答案
相关题目
 把“①等腰三角形、②等边三角形、③三角形”填入图中.(填序号)
把“①等腰三角形、②等边三角形、③三角形”填入图中.(填序号) 你能把一个等边三角形分成大小,形状都相同的3个,4个,6个三角形吗?
你能把一个等边三角形分成大小,形状都相同的3个,4个,6个三角形吗?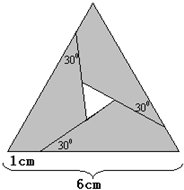 如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.
如图所示,把边长为6cm的等边三角形剪成4部分,从三角形顶点往下1cm处,呈30°角下剪刀,使中间部分形成一个小的等边三角形.