题目内容
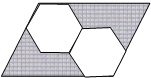 如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )
如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:由题中条件可得平行四边形中两边的阴影面积相等,则求解一个阴影的面积及平行四边形的面积即可得出两者之间的关系.
解答:解:如图,
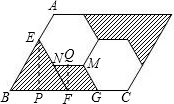
则S阴影=2(S△BEF+SFGMN),
设正六边形的边长为a,
由于正六边形的存在,所以∠BEF=60°,
则可得BE=EF=2a,BC=4a,AB=3a,
则在Rt△BEF中可得其高EP=
a,
同理可得FQ=
a,
∴S阴影=2(S△BEF+SFGMN),
=2(
?BF?EP+FG?FQ),
=2(
?2a?
a+
a?a),
=3
a2,
而SABCD=BC?h=4a?
a=6
a2,
∴S阴影=
SABCD,
故选:A.

则S阴影=2(S△BEF+SFGMN),
设正六边形的边长为a,
由于正六边形的存在,所以∠BEF=60°,
则可得BE=EF=2a,BC=4a,AB=3a,
则在Rt△BEF中可得其高EP=
| 3 |
同理可得FQ=
| ||
| 2 |
∴S阴影=2(S△BEF+SFGMN),
=2(
| 1 |
| 2 |
=2(
| 1 |
| 2 |
| 3 |
| ||
| 2 |
=3
| 3 |
而SABCD=BC?h=4a?
3
| ||
| 2 |
| 3 |
∴S阴影=
| 1 |
| 2 |
故选:A.
点评:本题主要考查的平行四边形的性质,正六边形的角度及对称问题,能够熟练求解.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
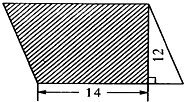 如图所示,平行四边形的面积是180平方分米,求空白部分的面积.
如图所示,平行四边形的面积是180平方分米,求空白部分的面积. 计算如图所示每个平行四边形的面积,你发现了什么?
计算如图所示每个平行四边形的面积,你发现了什么? 动手画一画:
动手画一画: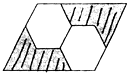 如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )
如图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的( )