题目内容
我会算
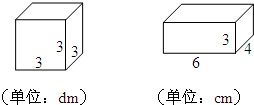
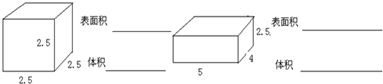
(1)求下面长方体和正方体的表面积和体积,单位:厘米
(2)用短除法求下列各组数的最大公约数或最小公倍数.

(3)下图是某校课外活动小组人数情况的统计图,看图回答问题.

①图中每个小格代表
②各小组中人数最多的是
③参加篮球组的人数比参加书法组的多
④根据以上条形统计图填写下面的统计表(单位:人).
(1)求下面长方体和正方体的表面积和体积,单位:厘米

(2)用短除法求下列各组数的最大公约数或最小公倍数.

(3)下图是某校课外活动小组人数情况的统计图,看图回答问题.

①图中每个小格代表
10人
10人
.②各小组中人数最多的是
绘画
绘画
组,人数最少的是舞蹈
舞蹈
组.③参加篮球组的人数比参加书法组的多
20
20
人.④根据以上条形统计图填写下面的统计表(单位:人).
| 绘画组 | 舞蹈组 | 篮球组 | 书法组 | 合唱组 | 合计 |
分析:(1)正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长;长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高;由此代入数据即可解答.
(2)求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数的连乘积;对于三个数来说:三个数的公有质因数连乘积是最大公约数,三个数的公有质因数、两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可.
(3)①根据纵轴上的数量进行计算,每两个格表示20人,所以可求出一个格代表多少人;
②通过观察,条形统计图中条形最高的人数最多,最低的人数最少;
③用参加篮球组的人数减去参加书法组的人数,就是参加篮球组的人数比参加书法组的多的人数;
④根据统计表各组的人数,完成统计表,并求出一共有多少人.
(2)求最大公约数也就是这几个数的公有质因数的连乘积,最小公倍数是公有质因数与独有质因数的连乘积;对于三个数来说:三个数的公有质因数连乘积是最大公约数,三个数的公有质因数、两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数,由此解决问题即可.
(3)①根据纵轴上的数量进行计算,每两个格表示20人,所以可求出一个格代表多少人;
②通过观察,条形统计图中条形最高的人数最多,最低的人数最少;
③用参加篮球组的人数减去参加书法组的人数,就是参加篮球组的人数比参加书法组的多的人数;
④根据统计表各组的人数,完成统计表,并求出一共有多少人.
解答:解:(1)正方体的表面积是:2.5×2.5×6=37.5(平方厘米);
体积是:2.5×2.5×2.5=15.625(立方厘米);
长方体的表面积是:(5×4+5×2.5+4×2.5)×2,
=(20+12.5+10)×2,
=42.5×2,
=85(平方厘米);
体积是:5×4×2.5=50(立方厘米).
答:正方体的表面积是37.5平方厘米,体积是15.625立方厘米;长方体的表面积是85平方厘米,体积是50立方厘米.
(2)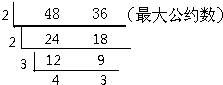
所以48和36的最大公约数是:2×2×3=12.
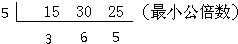
所以15、30和25的最小公倍数是:5×3×6×5=450,
答:48和36的最大公约数是12;15、30和25的最小公倍数是:450.
(3)由题意和统计图可知:
①20÷2=10(人).
答:图中每个小格代表10人.
②通过观察,条形统计图中条形最高的人数最多,最低的人数最少,
所以各小组中人数最多的是绘画组,人数最少的是舞蹈组.
③90-70=20(人).
答:参加篮球组的人数比参加书法组的多 20人.
④根据统计表各组的人数,完成统计表如下:
故答案为:10人,绘画,舞蹈,20.
体积是:2.5×2.5×2.5=15.625(立方厘米);
长方体的表面积是:(5×4+5×2.5+4×2.5)×2,
=(20+12.5+10)×2,
=42.5×2,
=85(平方厘米);
体积是:5×4×2.5=50(立方厘米).
答:正方体的表面积是37.5平方厘米,体积是15.625立方厘米;长方体的表面积是85平方厘米,体积是50立方厘米.
(2)

所以48和36的最大公约数是:2×2×3=12.
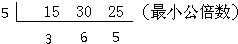
所以15、30和25的最小公倍数是:5×3×6×5=450,
答:48和36的最大公约数是12;15、30和25的最小公倍数是:450.
(3)由题意和统计图可知:
①20÷2=10(人).
答:图中每个小格代表10人.
②通过观察,条形统计图中条形最高的人数最多,最低的人数最少,
所以各小组中人数最多的是绘画组,人数最少的是舞蹈组.
③90-70=20(人).
答:参加篮球组的人数比参加书法组的多 20人.
④根据统计表各组的人数,完成统计表如下:
| 绘画组 | 舞蹈组 | 篮球组 | 书法组 | 合唱组 | 合计 |
| 110 | 60 | 90 | 70 | 100 | 430 |
点评:(1)考查了长方体和正方体的表面积与体积公式的计算应用.
(2)主要考查求两个数的最大公约数与三个数的最小公倍数的方法,除了用短除法外还可以用分解质因数的方法.
(3)考查了从统计图中获取信息并解决问题.
(2)主要考查求两个数的最大公约数与三个数的最小公倍数的方法,除了用短除法外还可以用分解质因数的方法.
(3)考查了从统计图中获取信息并解决问题.

练习册系列答案
相关题目