题目内容
有两个相同大小的长方体木块,长、宽、高分别是10厘米、6厘米、8厘米.把一个加工成最大的正方体,另一块加工成最大的圆柱体,那么加工后的正方体与圆柱体的表面积之比是多少?如果再把正方体和圆柱体分别加工成最大的圆锥体,那么两个圆锥体的体积之比是多少?
解:(1)正方体的表面积是:6×6×6=216(平方厘米),
圆柱的表面积是:3.14×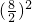 ×2+3.14×8×6,
×2+3.14×8×6,
=100.48+150.72,
=251.2(平方厘米),
所以加工后的正方体与圆柱体的表面积之比是216:251.2=135:157;
答:加工后的正方体与圆柱体的表面积之比是135:157.
(2)正方体内最大的圆锥的体积是: ×3.14×
×3.14× ×6,
×6,
=3.14×9×2,
=56.52(立方厘米),
圆柱内最大的圆锥的体积是:3.14×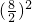 ×6÷3,
×6÷3,
=3.14×16×2,
=100.48(立方厘米),
56.52:100.48=1413:2512,
答:再把正方体和圆柱体分别加工成最大的圆锥体,那么两个圆锥体的体积之比是1413:2512.
分析:(1)长方体内最大的正方体的棱长,是这个长方体最短的边长,所以加工出的正方体的棱长是6厘米;
根据长方体内最大的圆柱的特点,这个长方体内最大的圆柱的底面直径是8厘米,高是6厘米;由此利用正方体和圆柱的表面积公式解解答;
(2)正方体内最大的圆锥的底面直径和高都等于这个正方体的棱长,由此利用圆锥的体积公式即可求出正方体内最大的圆锥的体积;
圆柱内最大的圆锥的体积等于这个圆锥的体积的 ,由此根据圆柱的体积公式的求出这个圆柱的体积,再除以3即可,由此即可解答.
,由此根据圆柱的体积公式的求出这个圆柱的体积,再除以3即可,由此即可解答.
点评:此题考查了正方体、圆柱、圆锥的体积公式的灵活应用,关键是抓住长方体内最大的正方体和最大的圆柱体,正方体内最大的圆锥,圆柱内最大的圆锥的特点进行解答.
圆柱的表面积是:3.14×
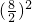 ×2+3.14×8×6,
×2+3.14×8×6,=100.48+150.72,
=251.2(平方厘米),
所以加工后的正方体与圆柱体的表面积之比是216:251.2=135:157;
答:加工后的正方体与圆柱体的表面积之比是135:157.
(2)正方体内最大的圆锥的体积是:
 ×3.14×
×3.14× ×6,
×6,=3.14×9×2,
=56.52(立方厘米),
圆柱内最大的圆锥的体积是:3.14×
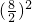 ×6÷3,
×6÷3,=3.14×16×2,
=100.48(立方厘米),
56.52:100.48=1413:2512,
答:再把正方体和圆柱体分别加工成最大的圆锥体,那么两个圆锥体的体积之比是1413:2512.
分析:(1)长方体内最大的正方体的棱长,是这个长方体最短的边长,所以加工出的正方体的棱长是6厘米;
根据长方体内最大的圆柱的特点,这个长方体内最大的圆柱的底面直径是8厘米,高是6厘米;由此利用正方体和圆柱的表面积公式解解答;
(2)正方体内最大的圆锥的底面直径和高都等于这个正方体的棱长,由此利用圆锥的体积公式即可求出正方体内最大的圆锥的体积;
圆柱内最大的圆锥的体积等于这个圆锥的体积的
 ,由此根据圆柱的体积公式的求出这个圆柱的体积,再除以3即可,由此即可解答.
,由此根据圆柱的体积公式的求出这个圆柱的体积,再除以3即可,由此即可解答.点评:此题考查了正方体、圆柱、圆锥的体积公式的灵活应用,关键是抓住长方体内最大的正方体和最大的圆柱体,正方体内最大的圆锥,圆柱内最大的圆锥的特点进行解答.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
计算下列各题,能简算的要简算.
| 224÷[56×(38-37)] | 34×(12÷68) | 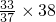 |
| (45+14)÷73+710 | 1.5×7.4+0.6×150%+2÷ . . |