题目内容
从图a那样的等边三角形开始,将三角形的每条边三等分,然后以中间的线段为边向外作新的等边三角形,如图b,得到一个“雪花六角形”.接着将“雪花六角形”的12条边的每一条三等分,仍以中间的线段为边向外作新的等边三角形,如图c,得到一个新的“雪花形”.问:图c的面积与图a的面积的比是多少?


分析:设图a的等边三角形的面积是l,在图b中,每条边上增加的等边三角形的面积是
.共增加了3个等边三角形,所以即可求出图b的面积和图a的面积的比;同理,图c中外边缘增加的小等边三角形的面积是
×
=
,共增加了12个小的等边三角形,进而求出图c的面积,问题得解.
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 81 |
解答:解:设图a的等边三角形的面积是l,在图b中,每条边上增加的等边三角形的面积是
,
共增加了3个等边三角形,所以图b的面积是1+3×
=
,图b的面积和图a的面积的比,4:3.
类似地,图c中外边缘增加的小等边三角形的面积是
×
=
,
共增加了12个小的等边三角形,
所以图c的面积是
+12×
=
+
=
.
所以,图c的面积和图a的面积比是
:1=40:27.
| 1 |
| 9 |
共增加了3个等边三角形,所以图b的面积是1+3×
| 1 |
| 9 |
| 4 |
| 3 |
类似地,图c中外边缘增加的小等边三角形的面积是
| 1 |
| 9 |
| 1 |
| 9 |
| 1 |
| 81 |
共增加了12个小的等边三角形,
所以图c的面积是
| 4 |
| 3 |
| 1 |
| 81 |
=
| 4 |
| 3 |
| 4 |
| 27 |
=
| 40 |
| 27 |
所以,图c的面积和图a的面积比是
| 40 |
| 27 |
点评:此题主要考查等积变形问题,利用边长的特点,求出各自的面积,问题即可得解.

练习册系列答案
相关题目
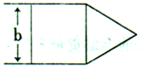 如图由正方形和等边三角形组成,它的周长是( )
如图由正方形和等边三角形组成,它的周长是( )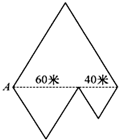 利民小区有一个由三个大小不同的等边三角形组成的绿化美化园区(如图),从A点出发,绕绿化美化园区走一周有多远?
利民小区有一个由三个大小不同的等边三角形组成的绿化美化园区(如图),从A点出发,绕绿化美化园区走一周有多远?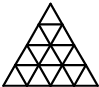 用30根等长的小棍拼成如图所示的等边三角形,图中有
用30根等长的小棍拼成如图所示的等边三角形,图中有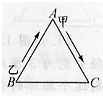 如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发
如图所示是一个边长为120m的等边三角形,甲乙同时分别从A点,B点按顺时针方向出发,甲每分钟走120m,乙每分钟走180m,但经过每个顶点时,因转弯都要耽误5s,则乙出发