题目内容
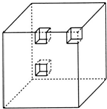 如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,挖掉的小立方体的棱长是________厘米.
如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,挖掉的小立方体的棱长是________厘米.
3
分析:根据题干可得原来正方体的表面积是20×20×6=2400平方厘米,在角上挖掉一个小正方体,表面积减少三个面的同时,也增加了3个面,所以表面积不变;在棱上挖掉一个小正方体,表面积比原来增加2个正方体的面;从面上挖掉一个小正方体,会增加4个小正方体的面,据此分析,挖掉后,一共要增加2+4=6个小正方体的面,据此求出一个面的面积,再根据完全平方数的特点,即可求出小正方体的边长.
解答:根据题干分析可得:在角上挖掉小正方体后,表面积不变;
在棱长上挖掉小正方体后,表面积比原来增加了2个面;
在面上挖掉小正方体后,表面积比原来增加了4个面;
(2454-20×20×4)÷(2+4),
=(2454-2400)÷6
=54÷6,
=9(平方厘米),
又因为3×3=9,
所以,挖掉的小正方体的棱长是3厘米.
答:挖掉的小正方体的棱长是3厘米.
故答案为:3.
点评:这道题是计算正方体的表面积的应用,在计算时要注意计算正方体缺少的是哪几个个面,从而列式解答即可.
分析:根据题干可得原来正方体的表面积是20×20×6=2400平方厘米,在角上挖掉一个小正方体,表面积减少三个面的同时,也增加了3个面,所以表面积不变;在棱上挖掉一个小正方体,表面积比原来增加2个正方体的面;从面上挖掉一个小正方体,会增加4个小正方体的面,据此分析,挖掉后,一共要增加2+4=6个小正方体的面,据此求出一个面的面积,再根据完全平方数的特点,即可求出小正方体的边长.
解答:根据题干分析可得:在角上挖掉小正方体后,表面积不变;
在棱长上挖掉小正方体后,表面积比原来增加了2个面;
在面上挖掉小正方体后,表面积比原来增加了4个面;
(2454-20×20×4)÷(2+4),
=(2454-2400)÷6
=54÷6,
=9(平方厘米),
又因为3×3=9,
所以,挖掉的小正方体的棱长是3厘米.
答:挖掉的小正方体的棱长是3厘米.
故答案为:3.
点评:这道题是计算正方体的表面积的应用,在计算时要注意计算正方体缺少的是哪几个个面,从而列式解答即可.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
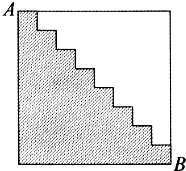 在一个边长为2.4米的正方形内,有条每小段长度都等于0.3米的折线(如图),求图中阴影部分的面积.
在一个边长为2.4米的正方形内,有条每小段长度都等于0.3米的折线(如图),求图中阴影部分的面积.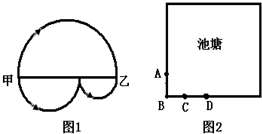 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).

 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).