题目内容
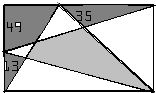 如图,在长方形内画了一些直线,已知边上三块带点图形的面积分别为13、35、49,则图中的阴影面积是
如图,在长方形内画了一些直线,已知边上三块带点图形的面积分别为13、35、49,则图中的阴影面积是分析:所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.
解答:解:设长方形的面积为S,则S△CDE=S△ABC=
S
由图形可知,S+S阴影=S△CDE+S△ABC+13+49+35
S阴影=
S+
S+13+49+35-S=97
故答案为:97.
| 1 |
| 2 |
由图形可知,S+S阴影=S△CDE+S△ABC+13+49+35
S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:97.
点评:本题考查长方形面积、三角形面积的计算.本题明白所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13、49、35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分是解决本题的关键,从而根据S+S阴影=S△CDE+S△ABC+13+49+35建立等量关系求解.

练习册系列答案
相关题目
