题目内容
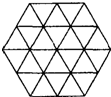 如图,一个边长是2的正六边形被分割成若干个边长是1的正三角形.则图中共有
如图,一个边长是2的正六边形被分割成若干个边长是1的正三角形.则图中共有38
38
个正三角形.分析:分别计算出边长为1的正三角形的个数个,边长为3的正三角形的个数,边长为2的正三角形的个数,然后相加即可得出正三角形总个数.
解答:解:边长为1的正三角形的有24个,边长为2的正三角形有12个,边长为3的正三角形的有2个,
共计24+12+2=38(个),
答:图中共有38个正三角形.
故答案为:38.
共计24+12+2=38(个),
答:图中共有38个正三角形.
故答案为:38.
点评:根据正三角形性质得出正三角形总个数是解题关键.

练习册系列答案
相关题目

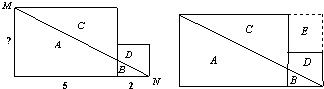 如图由一个边长为2厘米的正方形和一个长为5厘米的长方形拼成的,线段MN把它们各分成两部分.已知A、B两块的面积和是C、D两块面积和的1.5倍.请问:长方形的宽是多少厘米?
如图由一个边长为2厘米的正方形和一个长为5厘米的长方形拼成的,线段MN把它们各分成两部分.已知A、B两块的面积和是C、D两块面积和的1.5倍.请问:长方形的宽是多少厘米? 如图,一个边长是6cm的正方形,依次连接四条边的中点,得到图中阴影部分.
如图,一个边长是6cm的正方形,依次连接四条边的中点,得到图中阴影部分. 如图,一个边长是6cm的正方形,依次连接四条边的中点,得到图中阴影部分.
如图,一个边长是6cm的正方形,依次连接四条边的中点,得到图中阴影部分.