题目内容
11.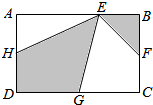 如图所示,长方形ABCD的面积为36平方厘米.H、F、G分别为AD、BC、CD的中点,E为AB边上的任意一点.求阴影部分的面积?
如图所示,长方形ABCD的面积为36平方厘米.H、F、G分别为AD、BC、CD的中点,E为AB边上的任意一点.求阴影部分的面积?
分析 如图,连结DE、CE,因为G为DC的中点,所以三角形EDG与三角形EGC的面积相等,因为F为BC的中点,所以三角形ECF与三角形EFB的面积相等,同理三角形EAH与三角形EHD的面积相等,因此,阴影部分和空白部分面积相等,都是长方形ABCD面积的一半.
解答 解:如图,连结DE、CE
由题意可知:三角形EDG与三角形EGC的面积相等
三角形ECF与三角形EFB的面积相等
三角形EAH与三角形EHD的面积相等,
所以阴影部分的面积为长方形ABCD面积的一半
36÷2=18(平方厘米)
答:阴影部分的面积是18平方厘米.
点评 等底等高的三角形面积相等,通过两条辅助线,就把这个长方形分成了6个三角形,每相邻的一个阴影三角形和空白三角形面积相等,因此,阴影部分、空白部分面积都是这个长方形面积的一半.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
2.某商品先加价10%后,再打九折出售,现价与原价相比,( )
| A. | 贵了 | B. | 便宜了 | C. | 没变化 | D. | 无法确 |
3.直接写出得数.
| 9-0.09= | 0.45×101= | 4.8×11-4.8= | 2÷0.02= |
| $\frac{1}{4}$×$\frac{2}{3}$= | 5-$\frac{2}{5}$= | 1-$\frac{1}{5}$+$\frac{4}{5}$= | 58÷1.2×($\frac{2}{5}$-40%)= |
1.一个正方体分割成两个长方体,表面积增加了40平方厘米,这个正方体原来的表面积是( )平方厘米.
| A. | 120 | B. | 180 | C. | 240 |