题目内容
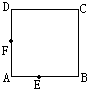 [最大面积].如图,正方形ABCD的边长是8厘米,E、F是边上的两点,且AE=3厘米,AF=4厘米.在正方形的边上再选择一点P,使得三角形EFP的面积尽可能大,那么最大的可能是多少?
[最大面积].如图,正方形ABCD的边长是8厘米,E、F是边上的两点,且AE=3厘米,AF=4厘米.在正方形的边上再选择一点P,使得三角形EFP的面积尽可能大,那么最大的可能是多少?
解:如图

三角形EFP的面积=正方形面积-三角形AEF面积-三角形BEC面积-三角形DFC面积
=8×8-3×4÷2-(8-4)×8÷2-(8-3)×8÷2,
=64-6-16-20,
=22cm2;
答:最大的可能是22cm2.
分析:因为三角形AEF是直角三角形,AE=3,AF=4,所以EF=5,三角形EFP的面积= ×EF×h
×EF×h
h是P点到EF的距离,所以要使三角形EFP的面积尽可能大,那么h应尽可能大.
C点到EF的距离最远,所以,P点应该选在C点,此时面积才最大.
三角形EFP的面积=正方形面积-三角形AEF面积-三角形BFC面积-三角形DEC面积,代入数值计算即可解答.
点评:解答本题的关键是找出符合条件的P点,然后根据面积公式计算.

三角形EFP的面积=正方形面积-三角形AEF面积-三角形BEC面积-三角形DFC面积
=8×8-3×4÷2-(8-4)×8÷2-(8-3)×8÷2,
=64-6-16-20,
=22cm2;
答:最大的可能是22cm2.
分析:因为三角形AEF是直角三角形,AE=3,AF=4,所以EF=5,三角形EFP的面积=
 ×EF×h
×EF×hh是P点到EF的距离,所以要使三角形EFP的面积尽可能大,那么h应尽可能大.
C点到EF的距离最远,所以,P点应该选在C点,此时面积才最大.
三角形EFP的面积=正方形面积-三角形AEF面积-三角形BFC面积-三角形DEC面积,代入数值计算即可解答.
点评:解答本题的关键是找出符合条件的P点,然后根据面积公式计算.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 (2008?丹阳市)张大伯用24米篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得最大面积,最大面积是( )平方米.
(2008?丹阳市)张大伯用24米篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得最大面积,最大面积是( )平方米.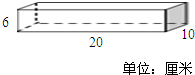 如图是一种饼干的包装盒,(1)请求出这种饼干盒的表面积;(2)如果将3盒这样的饼干包成一包(不计接口处),请计算出最节省的包装方法需要多大面积的包装纸?
如图是一种饼干的包装盒,(1)请求出这种饼干盒的表面积;(2)如果将3盒这样的饼干包成一包(不计接口处),请计算出最节省的包装方法需要多大面积的包装纸?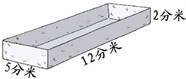 一个无盖的长方体铁皮水槽(如图),做这个水槽至少需要多大面积的铁皮?这个水槽最多可以盛水多少升?
一个无盖的长方体铁皮水槽(如图),做这个水槽至少需要多大面积的铁皮?这个水槽最多可以盛水多少升?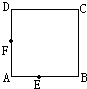 [最大面积].如图,正方形ABCD的边长是8厘米,E、F是边上的两点,且AE=3厘米,AF=4厘米.在正方形的边上再选择一点P,使得三角形EFP的面积尽可能大,那么最大的可能是多少?
[最大面积].如图,正方形ABCD的边长是8厘米,E、F是边上的两点,且AE=3厘米,AF=4厘米.在正方形的边上再选择一点P,使得三角形EFP的面积尽可能大,那么最大的可能是多少? 张大伯用24米长的篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得鸡栏面积最大,最大面积是( )平方米.
张大伯用24米长的篱笆靠一面墙围成一个长方形的养鸡栏(如图),要想围得鸡栏面积最大,最大面积是( )平方米.