题目内容
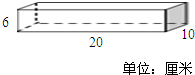 如图是一种饼干的包装盒,(1)请求出这种饼干盒的表面积;(2)如果将3盒这样的饼干包成一包(不计接口处),请计算出最节省的包装方法需要多大面积的包装纸?
如图是一种饼干的包装盒,(1)请求出这种饼干盒的表面积;(2)如果将3盒这样的饼干包成一包(不计接口处),请计算出最节省的包装方法需要多大面积的包装纸?分析:(1)求这种饼干盒的表面积,根据“长方体的表面积=(长×宽+长×高+宽×高)×2”代入数值,解答即可;
(2)把这3个长方体糖果盒的20×10面相粘合,得到的大长方体的表面积最小,比原来两个糖果盒的表面积减少了4个最大的面,最节约包装纸,由此即可解答.
(2)把这3个长方体糖果盒的20×10面相粘合,得到的大长方体的表面积最小,比原来两个糖果盒的表面积减少了4个最大的面,最节约包装纸,由此即可解答.
解答:解:(1)(20×10+20×6+10×6)×2,
=380×2,
=760(平方厘米);
答:这种饼干盒的表面积是760平方厘米;
(2)(20×10+20×6+10×6)×2×3-20×10×4,
=380×2×3-800,
=2280-800,
=1480(平方厘米);
答:最节省的包装方法需要1480平方厘米的包装纸.
=380×2,
=760(平方厘米);
答:这种饼干盒的表面积是760平方厘米;
(2)(20×10+20×6+10×6)×2×3-20×10×4,
=380×2×3-800,
=2280-800,
=1480(平方厘米);
答:最节省的包装方法需要1480平方厘米的包装纸.
点评:抓住两个长方体拼组一个大长方体的方法:最大面相粘合,得到的大长方体的表面积最小;最小面相粘合,得到的大长方体的表面积最大;用到的知识点:长方体表面积的计算方法.

练习册系列答案
相关题目