题目内容
17.(1)观察下面的图形,其中三角形和梯形的面积相等;平行四边形的面积最大.(2)如果在两条平行线间画一个和已知三角形面积相等的平行四边形,这个平行四边形的底是6厘米.
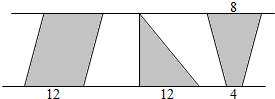
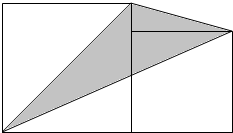
分析 (1)由图可知,三角形、平行四边形、梯形的高相等,设三个图形的高都是h,根据“三角形的面积=底×高÷2”求出三角形的面积;根据“平行四边形的面积=底×高”求出平行四边形的面积;根据“梯形的面积=(上底+下底)×高÷2”求出梯形的面积;进而比较即可得出结论;
(2)根据等底等高的三角形的面积是平行四边形面积的一半,所以在两条平行线间画一个和已知三角形面积相等的平行四边形,这个平行四边形的底是三角形底的一半,是12÷2=6厘米,由此解答即.
解答 解:(1)设高为x,
平行四边形:12x(平方厘米)
三角形:12x÷2=6x(平方厘米)
梯形:(8+4)x÷2=6x(平方厘米)
所以 三角形和 梯形的面积相等; 平行四边形的面积最大;
(2)12÷2=6(厘米)
答:这个平行四边形的底是 6厘米.
故答案为:三角形,梯形,平行四边形;6厘米.
点评 此题主要根据平行线的性质,得出梯形、三角形、平行四边形的高相等,再根据三角形、平行四边形和梯形的面积计算公式进行分析、比较即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.我国个人所得税法规定:个人月收入超过3500元的部分应缴个人所得税.张明的爸爸某月的收人是6000元,他应缴多少元个人所得税?(税率如表)
| 全月应纳税所得额 | 税率 |
| 不超过1500元的部分 | 3% |
| 超过1500元~4500元的部分 | 10% |
| 超过4500元~9000元的部分 | 20% |