题目内容
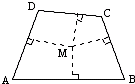 如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?
如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?
解:连接AM,BM,CM,DM得到四个三角形,如图:
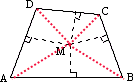
SABCD=S△ABM+S△BCM+S△CDM+S△DAM,
= AB×5.5+
AB×5.5+ BC×5.5+
BC×5.5+ CD×5.5+
CD×5.5+ DA×5.5,
DA×5.5,
= (AB+BC+CD+DA)×5.5,
(AB+BC+CD+DA)×5.5,
= ×60×5.5,
×60×5.5,
=165(平方厘米);
答:这个四边形的面积是165平方厘米.
故答案为:165.
分析:已知图中四边形ABCD的周长是60厘米,点M到各边的距离都是6.5厘米,可以把这个四边形分割转化为4个三角形,这4个三角形的底分别是四边形的4条边,高都是6.5厘米,根据三角形的面积计算公式,s= ah,求这4个三角形的面积之和即可.
ah,求这4个三角形的面积之和即可.
点评:此题解答关键是运用转化,将四边形ABCD分割转化为4个三角形,利用三角形的面积计算公式解决问题.

SABCD=S△ABM+S△BCM+S△CDM+S△DAM,
=
 AB×5.5+
AB×5.5+ BC×5.5+
BC×5.5+ CD×5.5+
CD×5.5+ DA×5.5,
DA×5.5,=
 (AB+BC+CD+DA)×5.5,
(AB+BC+CD+DA)×5.5,=
 ×60×5.5,
×60×5.5,=165(平方厘米);
答:这个四边形的面积是165平方厘米.
故答案为:165.
分析:已知图中四边形ABCD的周长是60厘米,点M到各边的距离都是6.5厘米,可以把这个四边形分割转化为4个三角形,这4个三角形的底分别是四边形的4条边,高都是6.5厘米,根据三角形的面积计算公式,s=
 ah,求这4个三角形的面积之和即可.
ah,求这4个三角形的面积之和即可.点评:此题解答关键是运用转化,将四边形ABCD分割转化为4个三角形,利用三角形的面积计算公式解决问题.

练习册系列答案
相关题目
 求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)
求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米) 如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?
如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?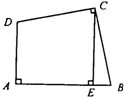 如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C到边AB的垂线CE长为10厘米,求四边形ABCD的面积.
如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C到边AB的垂线CE长为10厘米,求四边形ABCD的面积.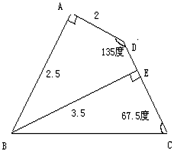 求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)
求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)