题目内容
 求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)
求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)
解:延长BA和CD相交于F点,因为∠BAD=∠FAD=90°,则∠AFD=∠ADF=(180°-90°)÷2=45°,所以三角形AFD是等腰直角三角形,那么AD=AF=2厘米,BF=BA+AF=2+2.5=4.5(厘米),因为三角形的内角和是180°,所以∠FBC=180°-∠FCB-∠BFC=180°-45°-67.5°=67.5°,所以∠FBC=∠FCB,三角形BFC是等腰三角形,那么BF=CF=4.5厘米,
所以四边形ABCD的面积,=三角形BCF面积-三角形ADF的面积,
=CF×BE÷2-AD×AF÷2,
=(2+2.5)×3.5÷2-2×2÷2,
=4.5×3.5÷2-2,
=7.875-2,
=5.875(平方厘米).
答:四边形ABCD的面积是5.875平方厘米.
分析:如图所示: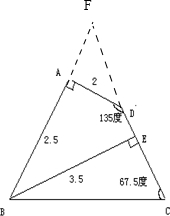 ,延长BA和CD相交于F点,因为∠BAD=∠FAD=90°,则∠AFD=∠ADF=(180°-90°)÷2=45°,所以三角形AFD是等腰直角三角形,那么AD=AF=2厘米,BF=BA+AF=2+2.5=4.5(厘米),因为三角形的内角和是180°,所以∠FBC=180°-∠FCB-∠BFC=180°-45°-67.5°=67.5°,所以∠FBC=∠FCB,三角形BFC是等腰三角形,那么BF=CF=4.5厘米,四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.
,延长BA和CD相交于F点,因为∠BAD=∠FAD=90°,则∠AFD=∠ADF=(180°-90°)÷2=45°,所以三角形AFD是等腰直角三角形,那么AD=AF=2厘米,BF=BA+AF=2+2.5=4.5(厘米),因为三角形的内角和是180°,所以∠FBC=180°-∠FCB-∠BFC=180°-45°-67.5°=67.5°,所以∠FBC=∠FCB,三角形BFC是等腰三角形,那么BF=CF=4.5厘米,四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.
点评:解决本题的关键是作出辅助线,推导出四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.
所以四边形ABCD的面积,=三角形BCF面积-三角形ADF的面积,
=CF×BE÷2-AD×AF÷2,
=(2+2.5)×3.5÷2-2×2÷2,
=4.5×3.5÷2-2,
=7.875-2,
=5.875(平方厘米).
答:四边形ABCD的面积是5.875平方厘米.
分析:如图所示:
 ,延长BA和CD相交于F点,因为∠BAD=∠FAD=90°,则∠AFD=∠ADF=(180°-90°)÷2=45°,所以三角形AFD是等腰直角三角形,那么AD=AF=2厘米,BF=BA+AF=2+2.5=4.5(厘米),因为三角形的内角和是180°,所以∠FBC=180°-∠FCB-∠BFC=180°-45°-67.5°=67.5°,所以∠FBC=∠FCB,三角形BFC是等腰三角形,那么BF=CF=4.5厘米,四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.
,延长BA和CD相交于F点,因为∠BAD=∠FAD=90°,则∠AFD=∠ADF=(180°-90°)÷2=45°,所以三角形AFD是等腰直角三角形,那么AD=AF=2厘米,BF=BA+AF=2+2.5=4.5(厘米),因为三角形的内角和是180°,所以∠FBC=180°-∠FCB-∠BFC=180°-45°-67.5°=67.5°,所以∠FBC=∠FCB,三角形BFC是等腰三角形,那么BF=CF=4.5厘米,四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.点评:解决本题的关键是作出辅助线,推导出四边形ABCD的面积=三角形BCF面积-三角形ADF的面积,计算即可.

练习册系列答案
相关题目
 求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米)
求如图四边形ABCD的面积.已知∠BAD=90度,BE为CD的高(单位:厘米) 如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?
如图四边形ABCD的周长是60厘米,M到各边的距离都是5.5厘米,求四边形ABCD的面积是多少平方厘米?
 如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C到边AB的垂线CE长为10厘米,求四边形ABCD的面积.
如图四边形ABCD中,角DAB和角DCB都是直角,边CD和边BC的长度相等,从点C到边AB的垂线CE长为10厘米,求四边形ABCD的面积.