题目内容
【题目】课外拓展

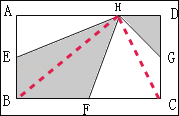
如图所示,长方形ABCD的面积为36平方厘米,E、F、G分别为边AB、BC、CD的中点,H为AD边上任意一点,问阴影部分的面积是多少?
【答案】阴影部分的面积是18平方厘米
【解析】
试题分析:如图,连接HB、HC,根据在三角形中等底同高的性质,三角形BHF与三角形FHC的面积相等,三角形HCG与三角形HGD的面积相等,三角形AEH与三角形EBH的面积相等,所以阴影部分的面积就是长方形ABCD的面积的一半.
解答:解:因为三角形BHF与三角形FHC的面积相等,三角形HCG与三角形HGD的面积相等,三角形AEH与三角形EBH的面积相等,
所以阴影部分的面积为:36÷2=18(平方厘米);
答:阴影部分的面积是18平方厘米.

练习册系列答案
相关题目

