Question

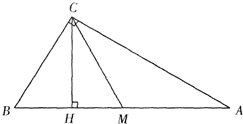如图，△ABC中，∠C是直角，AB边上的高CH和中线CM三等分∠C．若△CHM之面积为24，那么△ABC之面积是多少？

Answer 1

分析：△ABC中，∠BCA是直角，所以△ABC是直角三角形，因为CM是斜边上的中线，所以CM=

1

2

AB；而CH和CM把∠BCA三等分，所以∠HCM=30°，HM=

1

2

CM，所以AB=4HM，S_△CHM=

1

2

CH×HM=24，而S_△ABC=

1

2

CH×AB=

1

2

CH×4HM=24×4=96．

解答：解：因为CM是RT△ABC斜边上的中线，
所以CM=

1

2

AB；
而CH和CM把∠BCA三等分，
所以∠HCM=30°，
HM=

1

2

CM，所以AB=4HM，
S_△CHM=

1

2

CH×HM=24，
S_△ABC=

1

2

CH×AB
=

1

2

CH×HM×4
=24×4
=96．
答：△ABC的面积是96．

点评：本题考查了直角三角形斜边上的中线等于斜边的一半的性质，以及直角三角形30°角所对的直角边等于斜边的一半的性质．