题目内容
如图，△ABC中，点E在AB上，点F在AC上，BF与CE相交于点P，如果S四边形AEPF=S△BEP等于S△CFP=4，则S△BPC的面积是
12
12
．分析：连接EF，AP，不难得出EF∥BC，且AP平分了四边形AEPF，然后利用题干中的已知条件和高一定时，面积与底成正比的关系得出：AF：FC=1：2，由此即可求得△BPC的面积．
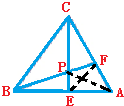
解答：解：连接EF，AP，
根据题干不难得出△CEF与△BEF面积相等且又同底，所以它们的底EF上的高也相等，由此可以得出：EF∥BC，则：CF：AF=BE：AE；
而CF：AF=S△CFP：S△AFP；BE：AE=S△BEP：S△AEP；
可得：S△CFP：S△AFP=S△BEP：S△AEP；
又因为S△CFP=S△BEP=4；所以可得AP平分了四边形AEPF，即：S△AFP=S△AEP=2；
所以可得：AF：FC=1：2，所以S△BAF：S△BFC=1：2，
所以△BPC的面积为：4×2×2-4=12，
故答案为：12．
根据题干不难得出△CEF与△BEF面积相等且又同底，所以它们的底EF上的高也相等，由此可以得出：EF∥BC，则：CF：AF=BE：AE；
而CF：AF=S△CFP：S△AFP；BE：AE=S△BEP：S△AEP；
可得：S△CFP：S△AFP=S△BEP：S△AEP；
又因为S△CFP=S△BEP=4；所以可得AP平分了四边形AEPF，即：S△AFP=S△AEP=2；
所以可得：AF：FC=1：2，所以S△BAF：S△BFC=1：2，
所以△BPC的面积为：4×2×2-4=12，
故答案为：12．
点评：此题考查了高一定时，三角形的面积与底成正比的关系的灵活应用，辅助线的连接是本题的关键．
练习册系列答案
相关题目
如图，在△ABC中，点D在BC上，且∠ABC=∠ACB，∠ADC=∠DAC，∠DAB=24°，求∠ABC的度数；并且回答：图中哪些三角形是钝角三角形？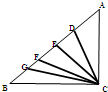
（2011?汉阳区）如图△ABC中，点D、E、F、G为AB边上四点，且
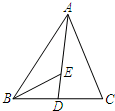如图：在△ABC中，点D为边BC的中点，点E为线段AD上一点，且满足AE=2ED，则△ABC的面积是△BDE的面积的