题目内容
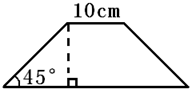 如图所示,已知等腰梯形的下底是上底的3倍,梯形的面积是
如图所示,已知等腰梯形的下底是上底的3倍,梯形的面积是200
200
cm2.分析:由图意可知:梯形的上底与它的高相等,又因“等腰梯形的下底是上底的3倍”,从而可以分别求出下底和高,进而利用梯形的面积=(上底+下底)×高÷2,即可求出这个梯形的面积.
解答:解:如图所示,作梯形的高DF,则BE=AE=FC=DF,
AD=EF,
又因AD=
BC,
所以AE=AD,
因此梯形的面积为:(10+10×3)×10÷2,
=40×10÷2,
=400÷2,
=200(平方厘米);
答:梯形的面积是200平方厘米.
故答案为:200.
AD=EF,
又因AD=
| 1 |
| 3 |
所以AE=AD,

因此梯形的面积为:(10+10×3)×10÷2,
=40×10÷2,
=400÷2,
=200(平方厘米);
答:梯形的面积是200平方厘米.
故答案为:200.
点评:此题主要考查梯形的面积的计算方法,关键是明白:梯形的上底与它的高相等.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
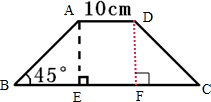
 (2011?毕节地区)如图所示,已知直角梯形的高为30厘米,∠1=∠2=45°,求梯形ABCD的面积.
(2011?毕节地区)如图所示,已知直角梯形的高为30厘米,∠1=∠2=45°,求梯形ABCD的面积.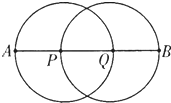 两个大小相同的圆,圆心分别为P、Q,如图所示.已知线段AB的长为15cm,求圆的半径和周长.
两个大小相同的圆,圆心分别为P、Q,如图所示.已知线段AB的长为15cm,求圆的半径和周长.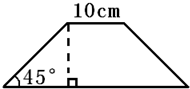 如图所示,已知等腰梯形的下底是上底的3倍,梯形的面积是________cm2.
如图所示,已知等腰梯形的下底是上底的3倍,梯形的面积是________cm2. 如图所示,已知直角梯形的高为30厘米,∠1=∠2=45°,求梯形ABCD的面积.
如图所示,已知直角梯形的高为30厘米,∠1=∠2=45°,求梯形ABCD的面积.