Question

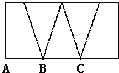
【题目】如图，虚线的“W”把一个长方形分成面积相等的五小块且两块梯形的形状完全相同，那么图中AB：BC的值为　 　．

Answer 1

【答案】．

【解析】

试题分析：根据“把一个长方形分成面积相等的五小块”，可知梯形ABED和三角形BCF的面积相等，进而根据它们的面积公式可得出DE=BC﹣AB；再根据长方形的对边相等，可得出2DE+2BC=2AB+BC；然后把DE=BC﹣AB代入2DE+2BC=2AB+BC中，求出AB与BC的比，进而求得比值即可．

解：见下图：

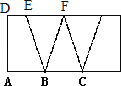
因为（DE+AB）×DA÷2=BC×DA÷2，

所以DE+AB=BC，DE=BC﹣AB；

又因为2DE+2BC=2AB+BC，

把DE=BC﹣AB代入2DE+2BC=2AB+BC中，得：

2BC﹣2AB+2BC=2AB+BC，

2BC+2BC﹣BC=2AB+2AB，

3BC=4AB，

所以AB：BC=3：4=3÷4=；