题目内容
有5个长方形，它们的长和宽都是整数，且5个长和5个宽恰好是1～10这10个整数；现在用这5个长方形拼成1个大正方形，那么，大正方形面积的最小值为（ ）
分析：先确定出正方形的边长，再利用正方形的面积公式，即可求得其面积．由题意知，大正方形的面积应是5个长方形面积的和，则正方形的边长必定大于10，于是可求结果．
解答：解：如图所示，
，
于是可得：正方形的边长为11，则其面积为11×11=121．
答：大正方形面积的最小值为121．
故此题答案为：C．
，于是可得：正方形的边长为11，则其面积为11×11=121．
答：大正方形面积的最小值为121．
故此题答案为：C．
点评：此题主要考查正方形的面积公式及据条件找出合适的组合，就可以求解．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
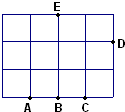（如图）由12个边长是1的小正方形拼成的长方形中有5个点，它们在小正方形的顶点上过其中的任意三点画三角形可以画
，商是多少？
的和是57，求这个数的50%是多少？
，再加1.25除以62.5%的商，和是多少？