题目内容
(1)用一根长12米的绳子围成一个封闭的四边形,可能有几种情况?填在下表里.
(2)用上面的绳子围成怎样的图形时,面积最大?最大的面积是多少?

(2)用上面的绳子围成怎样的图形时,面积最大?最大的面积是多少?
分析:(1)12米的绳子围成一个长方形,一条长与宽的和是6米,有以下几种情况:长5米宽1米、或长4米宽2米、或边长3米的正方形,据此即可解答.
(2)根据长方形和正方形的面积公式,把上述三种情况下的面积计算出来,即可解答.
(2)根据长方形和正方形的面积公式,把上述三种情况下的面积计算出来,即可解答.
解答:解:(1)根据题干分析有以下几种情况:长5米宽1米时:周长是12厘米,面积是5×1=5(平方厘米);
或长4米宽2米时:周长是12厘米,面积是4×2=8(平方厘米);
或边长3米的正方形时:周长是12厘米,面积是3×3=9(平方厘米);填表如下:
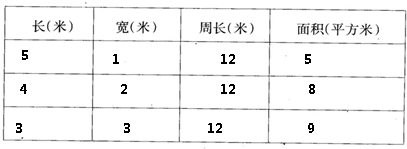
(2)由上述计算可得:围成正方形时,面积最大,是9平方厘米.
或长4米宽2米时:周长是12厘米,面积是4×2=8(平方厘米);
或边长3米的正方形时:周长是12厘米,面积是3×3=9(平方厘米);填表如下:

(2)由上述计算可得:围成正方形时,面积最大,是9平方厘米.
点评:此题考查了长方形、正方形的周长与面积公式的计算应用,关键是根据已知的绳子的长度明确长方形的长与宽的值.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
