题目内容
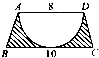
 如图,ABCD是梯形,AD平行于BC,BC=2AD,M是BC的中点,N是BM的中点,P是AD的中点,则△NCD的面积是△ANP的面积的多少倍?
如图,ABCD是梯形,AD平行于BC,BC=2AD,M是BC的中点,N是BM的中点,P是AD的中点,则△NCD的面积是△ANP的面积的多少倍?分析:由AD平行于BC,所以△NCD和△ANP等高,则面积的比就是底的比,即NC:AP的比,由BC=2AD,M是BC的中点,N是BM的中点,P是AD的中点,进行等量代换推出AP=BN=
BC,NC=
BC,得出NC:AP的比,从而得出面积的比.
| 1 |
| 4 |
| 3 |
| 4 |
解答:解:因为AD∥BC,
所以△NCD和△ANP等高,
所以S△NCD:S△ANP=NC:AP,
因为M是BC的中点,N是BM的中点,
NC=
BC,
又因为BC=2AD,P是AD的中点,
所以AP=
BC,
所以NC:AP=
BC:
BC,
NC:AP=3:1,
所以S△NCD:S△ANP=3:1,
所以S△NCD=3S△ANP.
答:△NCD的面积是△ANP的面积的3倍.
所以△NCD和△ANP等高,
所以S△NCD:S△ANP=NC:AP,
因为M是BC的中点,N是BM的中点,
NC=
| 3 |
| 4 |
又因为BC=2AD,P是AD的中点,
所以AP=
| 1 |
| 4 |
所以NC:AP=
| 3 |
| 4 |
| 1 |
| 4 |
NC:AP=3:1,
所以S△NCD:S△ANP=3:1,
所以S△NCD=3S△ANP.
答:△NCD的面积是△ANP的面积的3倍.
点评:此题考查了在高相等的情况下,三角形的面积比就是底的比,求S△NCD是S△ANP的几倍,利用条件找这两个三角形的底之间的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是
(2009?崇文区)如图,ABCD是直角梯形,已知OE垂直于DC,AD=10厘米,三角形BOC面积为15平方厘米,那么三角形ADO的面积是 如图,ABCD是梯形,E是AD的中点,直线CE把梯形分成甲乙两部分,它们的面积之比是
如图,ABCD是梯形,E是AD的中点,直线CE把梯形分成甲乙两部分,它们的面积之比是