题目内容

(2
3
4
×0.72+
7
25
×2.75)×[4.375-（2
3
8
+1
1
3
）]
[7
1
3
-(
49
12
-
63
20
+
77
30
-
91
42
+
105
56
)]÷22
1
3
+
1
3+6
+
1
3+6+9
+…+
1
3+6+9+…+96+99
．
分析：（1）运用乘法的分配律进行简算，
（2）原式=[7
1
3
-7×（
7
12
-
9
20
+
11
30
-
13
42
+
15
56
）]÷22=[7
1
3
-7×（
1
3
+
1
4
-
1
4
-
1
5
+
1
5
+
1
6
-
1
6
-
1
7
+
1
7
+
1
8
）]÷22，再进行简算，
（3）原式=
1
3
×[1+
1
1+2
+
1
1+2+3
+…+
1
1+2+3+…+32+33
]=
1
3
×（1+
2
2×3
+
2
3×4
+…+
2
33×34
）=
1
3
×[2×（1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…
1
33
-
1
34
）]，再进行简算．
解答：解：（1）(2
3
4
×0.72+
7
25
×2.75)×[4.375-（2
3
8
+1
1
3
），
=（2.75×0.72+0.28×2.75）×[4.375-（2.375+1
1
3
）]，
=[2.75×（0.72+0.28）]×[4.375-2.375+1
1
3
]，
=2.75×1×（2+1
1
3
），
=2.75×1×3
1
3
，
=
55
6
；

（2）[7
1
3
-(
49
12
-
63
20
+
77
30
-
91
42
+
105
56
)]÷22，
=[7
1
3
-7×（
7
12
-
9
20
+
11
30
-
13
42
+
15
56
）]÷22，
=[7
1
3
-7×（
1
3
+
1
4
-
1
4
-
1
5
+
1
5
+
1
6
-
1
6
-
1
7
+
1
7
+
1
8
）]÷22，
═[7
1
3
-7×（
1
3
+
1
8
）]÷22，
=（
22
3
-7×
11
24
）÷22，
=（
22
3
-
77
24
）÷22，
=
22
3
÷22-
77
24
÷22，
=
1
3
-
7
48
，
=
3
16
；


（3）
1
3
+
1
3+6
+
1
3+6+9
+…+
1
3+6+9+…+96+99
，
=
1
3
×[1+
1
1+2
+
1
1+2+3
+…+
1
1+2+3+…+32+33
]，
=
1
3
×（1+
2
2×3
+
2
3×4
+…+
2
33×34
），
=
1
3
×[2×（1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+…
1
33
-
1
34
）]，
=
1
3
×[2×（1-
1
34
）]，
=
1
3
×2×
33
34
，
=
11
17
．
点评：本题考查了分数、小数四则混合运算的定律，注意算式的特点，灵活运用运算定律进行简算．
练习册系列答案
相关题目
算一算
120×5=		 0+455= 400×8=
234×2= 5×40= 101×2=
99×2≈ 72×6≈ 351×3≈
计算
（1）（2
3
4
×0.72+
7
25
×2.75）×[4.375-（2
3
8
+1
1
3
）]
（2）（
11
12
-
7
6
+
3
4
-
17
24
）×（-48）
（3）-14+(1-0.5)×
1
3
×[2-(-3)2]．
在横线里填上＞、＜或=
72÷9= 29+39= 450-170= 50×2= 234×0= 6×8+3=
3000×3= 56÷8=
4
9
+
4
9
=		 1-
5
8
=
1
2
+
1
2
=
7
8
-
5
8
=

直接写出得数

72÷9=29+39=450-170=50×2=234×0=6×8+3=
3000×3=56÷8=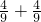数学公式=1-数学公式=数学公式+数学公式=数学公式-数学公式=

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网