Question

仔细观察：

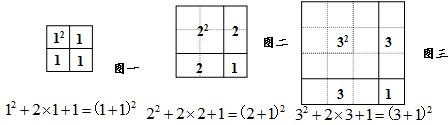
图四：

（1）你发现规律了吗？照样子在横线上写出第4个等式，并画出第4个图形；
（2）用含n的式子表示出第n个等式

n²+2n+1=（n+1）²

；
（3）请你借助发现的规律进行简便计算：1+2×999+999²=

1000000

．

Answer 1

分析：（1）根据给出的图形和等式作答；
（2）利用完全平方公式可以表示出第n个等式；
（3）利用（2）的规律求解即可．

解答：解：（1）如图所示：


（2）用含n的式子表示出第n个等式为：n²+2n+1=（n+1）²；

（3）1+2×999+999²，
=（1+999）²，
=1000²，
=1000000．
故答案为：；n²+2n+1=（n+1）²；1000000．

点评：考查了数表中的规律，根据给出的三个图形找到完全平方公式的规律：n²+2n+1=（n+1）²，再根据规律求解．