题目内容
直角梯形内接最大圆.(图略,圆形面积为空白部分)
梯形上底3厘米,下底3.7厘米,高3厘米,求周边阴影部分的面积.
解:(3+3.7)×3÷2-3.14×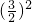 ,
,
=6.7×3÷2-3.14×2.25,
=20.1÷2-7.065,
=10.05-7.065,
=2.985(平方厘米);
答:阴影部分的面积是2.985平方厘米.
分析:如图所示,这个直角梯形内最大圆的直径就等于梯形的高,于是可得:阴影部分的面积=梯形的面积-圆的面积,梯形的上底、下底和高已知,分别利用梯形和圆的面积公式即可求解.

点评:此题主要考查梯形和圆的面积的计算方法,关键是明白:这个直角梯形内最大圆的直径就等于梯形的高.
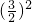 ,
,=6.7×3÷2-3.14×2.25,
=20.1÷2-7.065,
=10.05-7.065,
=2.985(平方厘米);
答:阴影部分的面积是2.985平方厘米.
分析:如图所示,这个直角梯形内最大圆的直径就等于梯形的高,于是可得:阴影部分的面积=梯形的面积-圆的面积,梯形的上底、下底和高已知,分别利用梯形和圆的面积公式即可求解.

点评:此题主要考查梯形和圆的面积的计算方法,关键是明白:这个直角梯形内最大圆的直径就等于梯形的高.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目