题目内容
18.在环形跑道上,两人同时同地都按顺时针方向跑时,每6分钟相遇一次,如果其余条件不变,其中一人改成按逆时针方向跑,每隔4分钟相遇一次,问两人各跑一圈需要几分钟?分析 把这个跑道的长度看作单位“1”,分别求得二人的速度,即可求出他们跑一圈各自用的时间:
(1)两人都按顺时针方向跑时,属于追及问题:假设两人为甲和乙,甲比乙跑的快,6分钟相遇说明二人的速度差是$\frac{1}{6}$;
(2)其中一人改成按逆时针方向跑,属于相遇问题:每隔4分钟相遇一次说明二人的速度之和是$\frac{1}{4}$;
有上述推理即可得出甲的速度为:($\frac{1}{6}$+$\frac{1}{4}$)÷2=$\frac{5}{24}$,从而得出乙的速度是:$\frac{1}{4}$-$\frac{5}{24}$=$\frac{1}{24}$;由此即可解决问题.
解答 解:甲的速度为:
($\frac{1}{6}$+$\frac{1}{4}$)÷2
=$\frac{5}{12}$÷2
=$\frac{5}{24}$
乙的速度是:
$\frac{1}{4}$-$\frac{5}{24}$=$\frac{1}{24}$
所以跑完一圈甲需要时间:1÷$\frac{5}{24}$=$\frac{24}{5}$(分钟)
乙跑完一圈需要时间:1÷$\frac{1}{24}$=24(分钟)
答:各跑一圈时,甲需要$\frac{24}{5}$分钟,乙需要24分钟.
点评 根据题干得出二人的速度之和与速度之差,从而得出他们各自的速度是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.同学们参加体操比赛,男生32人,女生24人,每8人1组,可分成( )组.
| A. | 7 | B. | 4 | C. | 13 |
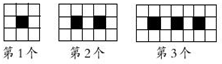 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第4个图案中白色正方形的个数为23;第n个图案中白色正方形的个数为5n+3.
下列图案由边长相等的黑、白两色正方形按一定规律拼接而成,依此规律,第4个图案中白色正方形的个数为23;第n个图案中白色正方形的个数为5n+3.