题目内容
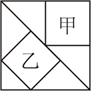 如图是一个正方形,甲和乙分别是等腰三角形的两种不同的内接正方形,则图中甲与乙的面积比是________.
如图是一个正方形,甲和乙分别是等腰三角形的两种不同的内接正方形,则图中甲与乙的面积比是________.
9:8
分析: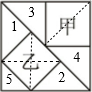
等腰直角三角形1、2的面积都是小正方形乙的 ,等腰直角三角形中5的面积是正方形乙的
,等腰直角三角形中5的面积是正方形乙的 ,可以求出正方形乙占大三角形的比例;
,可以求出正方形乙占大三角形的比例;
等腰直角三角形3、4的面积都是小正方形甲的 ,可以求出正方形甲占大三角形的比例.
,可以求出正方形甲占大三角形的比例.
两个大三角形的面积相等.那么正方形甲和正方形乙的面积比即可求出.
解答:若设正方形乙面积为1,则大三角形的面积是:
1+ +
+ +
+ =
= ,
,
正方形乙占大三角形的比例为:
1÷ =
= ;
;
因为小三角形3、4的面积和等于正方形甲的面积,所以正方形甲占大三角形的比例是 ;
;
那么正方形甲和正方形乙的面积比为:
 :
: =(
=( ×18):(
×18):( ×18)=9:8.
×18)=9:8.
故答案为:9:8.
点评:此题考查了图形的拼组,找到一个相同量作为比较,是解决此题的关键.
分析:

等腰直角三角形1、2的面积都是小正方形乙的
 ,等腰直角三角形中5的面积是正方形乙的
,等腰直角三角形中5的面积是正方形乙的 ,可以求出正方形乙占大三角形的比例;
,可以求出正方形乙占大三角形的比例;等腰直角三角形3、4的面积都是小正方形甲的
 ,可以求出正方形甲占大三角形的比例.
,可以求出正方形甲占大三角形的比例.两个大三角形的面积相等.那么正方形甲和正方形乙的面积比即可求出.
解答:若设正方形乙面积为1,则大三角形的面积是:
1+
 +
+ +
+ =
= ,
,正方形乙占大三角形的比例为:
1÷
 =
= ;
;因为小三角形3、4的面积和等于正方形甲的面积,所以正方形甲占大三角形的比例是
 ;
;那么正方形甲和正方形乙的面积比为:
 :
: =(
=( ×18):(
×18):( ×18)=9:8.
×18)=9:8.故答案为:9:8.
点评:此题考查了图形的拼组,找到一个相同量作为比较,是解决此题的关键.

练习册系列答案
相关题目
 如图所示,已知四边形ABEF是一个正方形,并且AC=BD,那么两个阴影部分的面积相比( )
如图所示,已知四边形ABEF是一个正方形,并且AC=BD,那么两个阴影部分的面积相比( )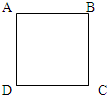 如图是一个边长为160米的正方形,甲、乙两人同时从A点出发,甲逆时针每分行75米,乙顺时针每分行45米.两人第一次在CD边(不在CD两点)上相遇,是出发后的( )次相遇.
如图是一个边长为160米的正方形,甲、乙两人同时从A点出发,甲逆时针每分行75米,乙顺时针每分行45米.两人第一次在CD边(不在CD两点)上相遇,是出发后的( )次相遇.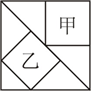 (2012?江汉区模拟)如图是一个正方形,甲和乙分别是等腰三角形的两种不同的内接正方形,则图中甲与乙的面积比是
(2012?江汉区模拟)如图是一个正方形,甲和乙分别是等腰三角形的两种不同的内接正方形,则图中甲与乙的面积比是 如图是一个边长为160米的正方形,甲、乙两人同时从A点出发,甲逆时针每分行75米,乙顺时针每分行45米.两人第一次在CD边(不在CD两点)上相遇,是出发后的次相遇.
如图是一个边长为160米的正方形,甲、乙两人同时从A点出发,甲逆时针每分行75米,乙顺时针每分行45米.两人第一次在CD边(不在CD两点)上相遇,是出发后的次相遇.