题目内容
 一个正三角形ABC,每边长1米,在每边上从顶点开始每隔2厘米取一点,然后从这些点出发作两条直线,分别和其他两边平行(如图).这些平行线相截在三角形ABC中得到许多边长为2厘米的正三角形.求边长为2厘米的正三角形的个数.
一个正三角形ABC,每边长1米,在每边上从顶点开始每隔2厘米取一点,然后从这些点出发作两条直线,分别和其他两边平行(如图).这些平行线相截在三角形ABC中得到许多边长为2厘米的正三角形.求边长为2厘米的正三角形的个数.分析:从图中不难看出边长为2厘米的三角形的个数:第一层有1个;第二层共有3个;第三层共有5个.于是想到共有几层,最底层共有多少个.由题意,正三角形ABC,每边长1米,在每边上从顶点开始每隔2厘米取一点,那么小三角形的层数是:100÷2=50.所以,边长为2厘米的三角形的个数实际上就是从1开始连续50个单数的和:1+3+5+…+99.计算这个等差数列的和即为所求小正三角形的个数.
解答:解:由题意及图示可得,边长为2厘米的正三角形的个数是:
1+3+5+…+99
=(1+99)×50÷2
=2500(个).
答:边长为2厘米的正三角形的个数是2500个.
1+3+5+…+99
=(1+99)×50÷2
=2500(个).
答:边长为2厘米的正三角形的个数是2500个.
点评:本题是一个难度较高的运用等差数列求解组合图形个数的应用题.解题关键是通过实际作图发现图形排列组合规律,并灵活运用等差数列的解题方法来解题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
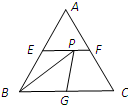 如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是
如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P线段EF上一个动点,连接BP、GP,则△BPG周长的最小值是
